题目内容
 如图,在△ACB中,∠ACB=90°,AC=BC,点C的坐标为(-2,0),点A的坐标为(-6,3),则B点的坐标是
如图,在△ACB中,∠ACB=90°,AC=BC,点C的坐标为(-2,0),点A的坐标为(-6,3),则B点的坐标是(1,5)
(1,5)
.分析:过A和B分别作AD⊥OC于D,BE⊥OC于E,利用已知条件可证明△ADC≌△CEB,再有全等三角形的性质和已知数据即可求出B点的坐标.
解答:解:过A和B分别作AD⊥OC于D,BE⊥OC于E,
∵∠ACB=90°,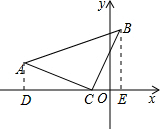
∴∠ACD+∠CAD=90°∠ACD+∠BCE=90°,
∴∠CAD=∠BCE,
在△ADC和△CEB中,
,
∴△ADC≌△CEB(AAS),
∴DC=BE,AD=CE,
∵点C的坐标为(-2,0),点A的坐标为(-6,3),
∴OC=1,AD=CD=3,OD=6,
∴CD=OD-OC=5,OE=CE-OC=3-2=1,
∴BE=5,
∴则B点的坐标是(1,5),
故答案为:(1,5).
∵∠ACB=90°,

∴∠ACD+∠CAD=90°∠ACD+∠BCE=90°,
∴∠CAD=∠BCE,
在△ADC和△CEB中,
|
∴△ADC≌△CEB(AAS),
∴DC=BE,AD=CE,
∵点C的坐标为(-2,0),点A的坐标为(-6,3),
∴OC=1,AD=CD=3,OD=6,
∴CD=OD-OC=5,OE=CE-OC=3-2=1,
∴BE=5,
∴则B点的坐标是(1,5),
故答案为:(1,5).
点评:本题借助于坐标与图形性质,重点考查了直角三角形的性质、全等三角形的判定和性质,解题的关键是做高线各种全等三角形.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
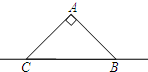 (2012•虹口区二模)如图,在△ACB中,∠CAB=90°,AC=AB=3,将△ABC沿直线BC平移,顶点A、C、B平移后分别记为A1、C1、B1,若△ACB与△A1C1B1重合部分的面积2,则CB1=
(2012•虹口区二模)如图,在△ACB中,∠CAB=90°,AC=AB=3,将△ABC沿直线BC平移,顶点A、C、B平移后分别记为A1、C1、B1,若△ACB与△A1C1B1重合部分的面积2,则CB1=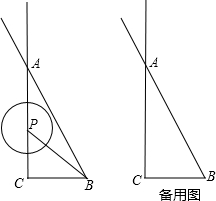 (2012•邯郸二模)如图,在△ACB中,∠ACB=90°,AC=4,BC=2,点P为射线CA上的一个动点,以P为圆心,1为半径作⊙P.
(2012•邯郸二模)如图,在△ACB中,∠ACB=90°,AC=4,BC=2,点P为射线CA上的一个动点,以P为圆心,1为半径作⊙P. 如图:在△ACB中,点D是AB边上一点,且∠ACB=∠CDA,∠CAB的平分线分别交CD、BC于点E、F.
如图:在△ACB中,点D是AB边上一点,且∠ACB=∠CDA,∠CAB的平分线分别交CD、BC于点E、F. 如图,在△ACB中,点D是AB边上的一点,且∠ACB=∠CDA;点E在BC边上,且点E到AC、AB的距离相等,连接AE交CD于点F.试判断△CEF的形状;并证明你的结论.
如图,在△ACB中,点D是AB边上的一点,且∠ACB=∠CDA;点E在BC边上,且点E到AC、AB的距离相等,连接AE交CD于点F.试判断△CEF的形状;并证明你的结论.