题目内容
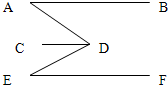40、已知：AB∥CD∥EF，你能得到∠ADE=∠A+∠E吗？请写出过程．分析：由AB∥CD∥EF，根据两直线平行，内错角相等，即可证得∠ADE=∠A+∠E．
解答：解：∵AB∥CD∥EF，
∴∠ADC=∠A，∠EDC=∠E，
∴∠ADE=∠ACD+∠ECD=∠A+∠E．
∴∠ADC=∠A，∠EDC=∠E，
∴∠ADE=∠ACD+∠ECD=∠A+∠E．
点评：此题考查了平行线的性质．解题的关键是注意掌握两直线平行，内错角相等定理的应用．
练习册系列答案
名校课堂系列答案
相关题目
18、如图，已知直线AB∥CD，∠DCF=110°，且AE=AF，求∠A的度数．
9、如图，已知直线AB∥CD，BE平分∠ABC，交CD于D，∠CDE=150°，则∠C的度数为（ ）
如图，直线AB、CD与直线EF分别交于E、F点，已知：AB∥CD，∠EFD的平分线FG交AB于点G，∠1=60°15′，则∠2=
如图，已知：AB∥CD，