题目内容
如图,在直角坐标系xOy中,二次函数y=x2+(2k﹣1)x+k+1的图象与x轴相交于O、A两点.

(1)求这个二次函数的解析式;
(2)在这条抛物线的对称轴右边的图象上有一点B,使△AOB的面积等于6,求点B的坐标;
(3)对于(2)中的点B,在此抛物线上是否存在点P,使∠POB=90°?若存在,求出点P的坐标,并求出△POB的面积;若不存在,请说明理由

(1)求这个二次函数的解析式;
(2)在这条抛物线的对称轴右边的图象上有一点B,使△AOB的面积等于6,求点B的坐标;
(3)对于(2)中的点B,在此抛物线上是否存在点P,使∠POB=90°?若存在,求出点P的坐标,并求出△POB的面积;若不存在,请说明理由
(1)y=x2﹣3x;(2)(4,4);(3)存在,点P 的坐标为(2,﹣2),△POB的面积是8.
试题分析:(1)将原点坐标代入抛物线中即可求出k的值,从而求得抛物线的解析式.
(2)根据(1)得出的抛物线的解析式可得出A点的坐标,也就求出了OA的长,根据△OAB的面积可求出B点纵坐标的绝对值,然后将符合题意的B点纵坐标代入抛物线的解析式中即可求出B点的坐标,然后根据B点在抛物线对称轴的右边来判断得出的B点是否符合要求即可.
(3)根据B点坐标可求出直线OB的解析式,由于OB⊥OP,由此可求出P点的坐标特点,代入二次函数解析式可得出P点的坐标.求△POB的面积时,求出OB,OP的长度即可求出△BOP的面积.
试题解析:
(1)∵函数的图象与x轴相交于O,∴0=k+1,∴k=﹣1.
∴这个二次函数的解析式为y=x2﹣3x.
(2)如图,过点B做BD⊥x轴于点D,
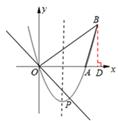
令x2﹣3x=0,解得:x=0或3.∴AO=3.
∵△AOB的面积等于6,∴AO•BD=6.∴BD=4.
∵点B在函数y=x2﹣3x的图象上,
∴4=x2﹣3x,解得:x=4或x=﹣1(舍去).
又∵顶点坐标为:( 1.5,﹣2.25),且2.25<4,
∴x轴下方不存在B点.
∴点B的坐标为:(4,4).
(3)存在.
∵点B的坐标为:(4,4),∴∠BOD=45°,.
若∠POB=90°,则∠POD=45°.
设P点坐标为(x,x2﹣3x).
∴.
若,解得x="4" 或x=0(舍去).此时不存在点P(与点B重合).
若,解得x="2" 或x=0(舍去).
当x=2时,x2﹣3x=﹣2.
∴点P的坐标为(2,﹣2).
∴.
∵∠POB=90°,∴△POB的面积为: PO•BO=××=8.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
 ,则该二次函数图象的顶点坐标是( )
,则该二次函数图象的顶点坐标是( ) 的图像过点(1,0)和(
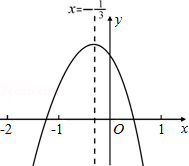
的图像过点(1,0)和( ,0),且
,0),且 ,现在有5个判断:(1)
,现在有5个判断:(1) (2)
(2) (3)
(3) (4)
(4) (5)
(5) ,请把你认为判断正确的序号写出来 .
,请把你认为判断正确的序号写出来 .
 与抛物线
与抛物线 交于点P,P点的纵坐标为-1,则关于x的方程
交于点P,P点的纵坐标为-1,则关于x的方程 的解是 .
的解是 .
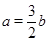 .
.
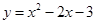 的顶点坐标是
的顶点坐标是