题目内容
【题目】如图,在△ABC中,∠B=45°, ![]() ,等腰直角△DAE中,∠DAE=90°,且点D是边BC上一点。
,等腰直角△DAE中,∠DAE=90°,且点D是边BC上一点。
(1)求AC的长;
(2)如图1,当点E恰在AC上时,求点E到BC的距离;
(3)如图2, 当点D从点B向点C运动时,求点E到BC的距离的最大值。

图1 图2
【答案】(1)4(2) ![]() (3)
(3) ![]()
【解析】试题分析:(1)作AF⊥BC,垂足为F,由已知可得BF=AF=2,从而得CF=BC-BF=2![]() ,在Rt△FAC中,利用勾股定理即可求出AC长;
,在Rt△FAC中,利用勾股定理即可求出AC长;
(2)过点A作AB的垂线交BC于点G,连接EG,证明△BAD≌△GAE,从而得∠AGE=∠ABD=45°,EG=BD,继而得∠EGB=90°,得到点E到BC的距离为EG的长,设BD=x,则DF=2-x,CD=2![]() +2-x,在Rt△ADF中,AD2=AF2+DF2=22+(2-x)2, 在Rt△ADC中,AD2=CD2-AC2=(2
+2-x,在Rt△ADF中,AD2=AF2+DF2=22+(2-x)2, 在Rt△ADC中,AD2=CD2-AC2=(2![]() +2-x)2-42,从而解得x=
+2-x)2-42,从而解得x=![]() ,即得到点E到BC的距离;
,即得到点E到BC的距离;
(3)当点D从点B向点C运动时,由(2)知点E到BC的距离为EG的长,即为BD的长,从而得到最大值即为BC的长.
试题解析:(1)作AF⊥BC,垂足为F,
∵∠B=45°,∴△FBA为等腰直角三角形,
∴BF=AF,
∵AB=2![]() ,∴AF=BF=2,
,∴AF=BF=2,
∵BC=2![]() +2,∴CF=BC-BF=2
+2,∴CF=BC-BF=2![]() ,
,
在Rt△FAC中,AC=![]() =4;
=4;
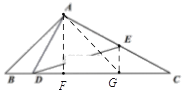
(2)过点A作AB的垂线交BC于点G,连接EG,
∵∠B=45°,∠BAG=90°,∴△GBA为等腰直角三角形,∴AB=AG, ∠AGB=45°,
∵∠DAE=90°,△DAE为等腰直角三角形,
∴AD=AE,∠BAD=∠GAE,∴△BAD≌△GAE,∴∠AGE=∠ABD=45°,EG=BD,
∴∠EGB=∠AGE+∠AGB=45°+45°=90°,故点E到BC的距离为EG的长,
设BD=x,则DF=2-x,CD=2![]() +2-x,
+2-x,
在Rt△ADF中,AD2=AF2+DF2=22+(2-x)2,
在Rt△ADC中,AD2=CD2-AC2=(2![]() +2-x)2-42,
+2-x)2-42,
∴22+(2-x)2=(2![]() +2-x)2-42,解得x=
+2-x)2-42,解得x=![]() ,
,
∴点E到BC的距离EG=BD=![]() ;
;
(3)当点D从点B向点C运动时,
由(2)可知△BAD≌△GAE,
∴∠AGE=∠ABD=45°,EG=BD,
∴∠EGB=∠AGE+∠AGB=45°+45°=90°,故点E到BC的距离为EG的长,
∵EG=BD,
∴当BD=BC=![]() 时,点E到BC的距离最大,最大值为
时,点E到BC的距离最大,最大值为![]() .
.

 名校课堂系列答案
名校课堂系列答案



