题目内容
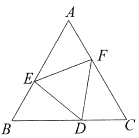
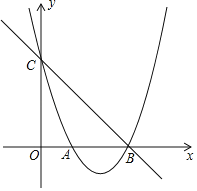
【题目】如图，已知二次函数y=ax2+bx+3的图象交x轴于点A（1，0），B（3，0），交y轴于点C．
（1）求这个二次函数的表达式；
（2）点P是直线BC下方抛物线上的一动点，求△BCP面积的最大值；
（3）直线x=m分别交直线BC和抛物线于点M，N，当△BMN是等腰三角形时，直接写出m的值．
【答案】（1）这个二次函数的表达式是y=x2﹣4x+3；（2）S△BCP最大=
；（3）当△BMN是等腰三角形时，m的值为
，﹣，1，2．
【解析】（1）根据待定系数法，可得函数解析式；
（2）根据平行于y轴直线上两点间的距离是较大的纵坐标减较小的纵坐标，可得PE的长，根据面积的和差，可得二次函数，根据二次函数的性质，可得答案；
（3）根据等腰三角形的定义，可得关于m的方程，根据解方程，可得答案．
（1）将A（1，0），B（3，0）代入函数解析式，得
，
解得
，
这个二次函数的表达式是y=x2-4x+3；
（2）当x=0时，y=3，即点C（0，3），
设BC的表达式为y=kx+b，将点B（3，0）点C（0，3）代入函数解析式，得
，
解这个方程组，得
直线BC的解析是为y=-x+3，
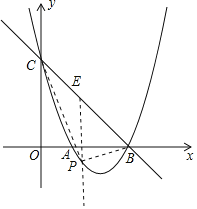
过点P作PE∥y轴
，
交直线BC于点E（t，-t+3），
PE=-t+3-（t2-4t+3）=-t2+3t，
∴S△BCP=S△BPE+SCPE=
（-t2+3t）×3=-
（t-）2+，
∵-＜0，∴当t=时，S△BCP最大=.
（3）M（m，-m+3），N（m，m2-4m+3）
MN=m2-3m，BM=|m-3|，
当MN=BM时，①m2-3m=（m-3），解得m=，
②m2-3m=-（m-3），解得m=-
当BN=MN时，∠NBM=∠BMN=45°，
m2-4m+3=0，解得m=1或m=3（舍）
当BM=BN时，∠BMN=∠BNM=45°，
-（m2-4m+3）=-m+3，解得m=2或m=3（舍），
当△BMN是等腰三角形时，m的值为，-，1，2．
