题目内容
【题目】如图（1）所示，已知四边形SBCD是由直角△SAB和直角梯形ABCD拼接而成的，其中∠SAB=∠SDC=90°，且点A为线段SD的中点，AD=2DC=1，AB=SD，现将△SAB沿AB进行翻折，使得二面角S﹣AB﹣C的大小为90°，得到的图形如图（2）所示，连接SC，点E、F分别在线段SB、SC上． 
（1）证明：BD⊥AF；
（2）若三棱锥B﹣AEC的体积是四棱锥S﹣ABCD体积的 
，求点E到平面ABCD的距离．
【答案】
（1）证明：∵四边形SBCD是由直角△SAB和直角梯形ABCD拼接而成的，其中∠SAB=∠SDC=90°，
二面角S﹣AB﹣C的大小为90°，
∴SA⊥AD，
又SA⊥AB，AB∩AD=A，∴SA⊥平面ABCD，
又BD平面ABCD，∴SA⊥BD，
在直角梯形ABCD中，∠BAD=∠ADC=90°，
AD=2CD=1，AB=2，
∴tan∠ABD=tan∠CAD= 
，
又∠DAC+∠BAC=90°，
∴∠ABD+∠BAC=90°，即AC⊥BD，
又AC∩SA=A，∴BD⊥平面SAC，
∵AF平面SAC，∴BD⊥AF．
（2）解：设点E到平面ABCD的距离为h，
∵VB﹣AEC=VE﹣ABC，且 
= 
，
∴ = 
= 
= ，
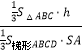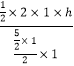解得h= ，
∴点E到平面ABCD的距离为 ．
【解析】（1）推导出SA⊥AD，SA⊥AB，从而SA⊥平面ABCD，进而SA⊥BD，再求出AC⊥BD，由此得到BD⊥平面SAC，从而能证明BD⊥AF．（2）设点E到平面ABCD的距离为h，由VB﹣AEC=VE﹣ABC ， 且 = ，能求出点E到平面ABCD的距离．
【考点精析】利用空间中直线与直线之间的位置关系对题目进行判断即可得到答案，需要熟知相交直线：同一平面内，有且只有一个公共点；平行直线：同一平面内，没有公共点；异面直线： 不同在任何一个平面内，没有公共点．
