题目内容
已知抛物线y=3x2-6x-9．
（1）求它的顶点坐标；
（2）求它与坐标轴的交点．
解：（1）∵y=3x2-6x-9
=3（x2-2x-3）
=3（x2-2x+1-4）
=y=3（x-1）2+12，
∴y=3x2-6x-9的顶点坐标为（1，12）；
（2）令y=0得：3x2-6x-9=0
解得：x=3或x=-1
故抛物线y=3x2-6x-9与x轴交与点（-1，0），（3，0）；
令x=0，解得y=-9，
故抛物线y=3x2-6x-9与y轴交与点（0，-9）．
分析：（1）将y=3x2-6x-9配方成3（x-1）2+12的形式即可确定其顶点坐标；
（2）分别令y=0和令x=0即可确定抛物线y=3x2-6x-9与坐标轴的交点坐标；
点评：本题考查了二次函数的性质及抛物线与坐标轴的交点坐标，解题的关键是正确的配方，这往往是解决二次函数问题的第一步．
=3（x2-2x-3）
=3（x2-2x+1-4）
=y=3（x-1）2+12，
∴y=3x2-6x-9的顶点坐标为（1，12）；
（2）令y=0得：3x2-6x-9=0
解得：x=3或x=-1
故抛物线y=3x2-6x-9与x轴交与点（-1，0），（3，0）；
令x=0，解得y=-9，
故抛物线y=3x2-6x-9与y轴交与点（0，-9）．
分析：（1）将y=3x2-6x-9配方成3（x-1）2+12的形式即可确定其顶点坐标；
（2）分别令y=0和令x=0即可确定抛物线y=3x2-6x-9与坐标轴的交点坐标；
点评：本题考查了二次函数的性质及抛物线与坐标轴的交点坐标，解题的关键是正确的配方，这往往是解决二次函数问题的第一步．
练习册系列答案
相关题目
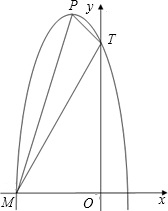如图，已知抛物线y=-3x2-（2c-b）x+a2，其中a、b、c是一个直角三角形的三边的长，且a＜b＜c，又知这个三角形两锐角的正弦值分别是方程25x2-35x+12=0的两个根．
如图，已知抛物线