题目内容
化简求值题:
(1)化简:
÷(x+2-
),然后请自选一个你喜欢的x值,再求原式的值.
(2)先化简,再求值:(
-
)÷
,其中x满足x2-x-1=0.
(1)化简:
| 4-x |
| x-2 |
| 12 |
| x-2 |
(2)先化简,再求值:(
| x-1 |
| x |
| x-2 |
| x+1 |
| 2x2-x |
| x2+2x+1 |
分析:(1)先把原式进行化简,再找出符合条件的x的值代入进行计算即可;
(2)先根据分式混合元算的法则把原式进行化简,再根据x2-x-1=0进行计算即可.
(2)先根据分式混合元算的法则把原式进行化简,再根据x2-x-1=0进行计算即可.
解答:解:(1)原式=
÷
=
×
=-
,
∵x-2≠0,x-4≠0,x+4≠0,
∴x=2,x=4,x=-4.
∴当x=1时,原式=-
=-
;
(2)原式=
÷
=
×
=
,
∵x2-x-1=0,
∴x2=x+1,
∴原式=
=
=1.
| 4-x |
| x-2 |
| x2-16 |
| x-2 |
=
| 4-x |
| x-2 |
| x-2 |
| (x+4)(x-4) |
=-
| 1 |
| x+4 |
∵x-2≠0,x-4≠0,x+4≠0,
∴x=2,x=4,x=-4.
∴当x=1时,原式=-
| 1 |
| 1+4 |
| 1 |
| 5 |
(2)原式=
| (x-1)(x+1)-x(x-2) |
| x(x+1) |
| 2x2-x |
| x2+2x+1 |
=
| 2x-1 |
| x(x+1) |
| (x+1)2 |
| x(2x-1) |
=
| x+1 |
| x2 |
∵x2-x-1=0,
∴x2=x+1,
∴原式=
| x+1 |
| x2 |
| x+1 |
| x+1 |
点评:本题考查的是分式的化简求值,在解答(1)时要注意x的值保证分式有意义;解答(2)时要注意用整体代入法.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
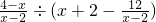 ,然后请自选一个你喜欢的x值,再求原式的值.
,然后请自选一个你喜欢的x值,再求原式的值.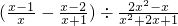 ,其中x满足x2-x-1=0.
,其中x满足x2-x-1=0.