题目内容
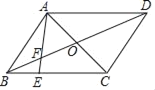
【题目】如图,在平行四边形ABCD中,AC,BD相交于点O,点E在BC上,AE交BD于F.
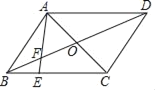
(1)若E是靠近点B的三等分点,求;①![]() 的值;②△BEF与△DAF的面积比;
的值;②△BEF与△DAF的面积比;
(2)当![]() 时,求
时,求![]() 的值.
的值.
【答案】(1)①![]() ;②
;②![]() ;(2)
;(2)![]() .
.
【解析】
(1)①利用平行线分线段成比例定理即可解决问题;
②利用相似三角形的中面积比等于相似比的平方即可解决问题;
(2)利用平行四边形的性质可知OB=OD,BC∥AD,BC=AD,由题意![]() 可知BF:DF=n:(2m+n),即BE:AD=BF:DF=n:(2m+n),故求得
可知BF:DF=n:(2m+n),即BE:AD=BF:DF=n:(2m+n),故求得![]() =
=![]() .
.
解:(1)①∵四边形ABCD是平行四边形,
∴BC=AD,BC∥AD,
∵BE:BC=1:3,
∴![]() =
=![]() =
=![]() .
.
②∵BE∥AD,
∴△BEF∽△DAF,
∴![]() (
(![]() )2=
)2=![]() .
.
(2)∵四边形ABCD是平行四边形,
∴OB=OD,BC∥AD,BC=AD,
∵BF:OF=n:m,
∴BF:DF=n:(2m+n),
∴BE:AD=BF:DF=n:(2m+n),
∴![]() =
=![]() .
.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目