题目内容
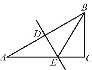
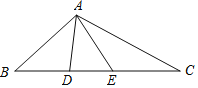
【题目】如图,![]() 为数轴上两条线段,其中
为数轴上两条线段,其中![]() 与原点重合,
与原点重合,![]() ,且
,且![]() .
.
(1)当![]() 为
为![]() 中点时,求线段
中点时,求线段![]() 的长;
的长;
(2)线段![]() 和
和![]() 以(1)中图形为初始位置,同时开展向右运动,线段
以(1)中图形为初始位置,同时开展向右运动,线段![]() 的运动速度为每秒5个单位长度,线段
的运动速度为每秒5个单位长度,线段![]() 运动速度为每秒3个单位长度,设运动时间为
运动速度为每秒3个单位长度,设运动时间为![]() 秒,请结合运动过程解决以下问题:
秒,请结合运动过程解决以下问题:
①当![]() 时,求
时,求![]() 的值;
的值;
②当![]() 时,请直接写出
时,请直接写出![]() 的值.
的值.

【答案】(1)AD=52;(2)①![]() 的值为2或18;②
的值为2或18;②![]() 的值为6或25.
的值为6或25.
【解析】
(1)求出BC,CD的值即可解决问题;
(2)①分点A在点C左侧时和点A在点C右侧时两种情况,分别根据![]() 列方程求解即可;
列方程求解即可;
②求出t秒后,A表示的数为5t,B表示的数为5t+10,C表示的数为3t+20,D表示的数为3t+52,根据![]() 列出绝对值方程,解方程即可.
列出绝对值方程,解方程即可.
解:(1)∵CD=3AB+2,AB=10,
∴CD=30+2=32,
∵![]() 为
为![]() 中点,即AB=CB=10,
中点,即AB=CB=10,
∴AD=AB+BC+CD=10+10+32=52;
(2)①当点A在点C左侧时,由题意得:3t+20-5t=16,
解得:t=2;
当点A在点C右侧时,由题意得:5t-3t-20=16,
解得:t=18,
故![]() 的值为2或18;
的值为2或18;
②由题意可得:t秒后,A表示的数为5t,B表示的数为5t+10,C表示的数为3t+20,D表示的数为3t+52,
∴![]() ,即
,即![]() ,
,
当![]() 时,可得
时,可得![]() ,
,
解得:![]() ;
;
当![]() 时,可得
时,可得![]() ,不符合题意;
,不符合题意;
当![]() 时,可得
时,可得![]() ,
,
解得:![]() ,
,
故![]() 的值为6或25.
的值为6或25.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】八(2)班组织了一次经典诵读比赛,甲、乙两队各10人的比赛成绩如下表(10分制):
甲 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
乙 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(1)甲队成绩的中位数是 分,乙队成绩的众数是 分;
(2)计算乙队的平均成绩和方差;
(3)已知甲队成绩的方差是1.4,则成绩较为整齐的是 队.
【题目】某班将举行知识竞赛活动,班长安排小明购买奖品.小明去文化用品店买了两种大小不同的笔记本一共a本,其中大笔记本单价8元,小笔记本单价5元.若设买单价5元小笔记本买了x本.
(1)填写下表:
单价(元/本) | 数量(本) | 金额(元) | |
小笔记本 | 5 | x | 5x |
大笔记本 | 8 |
(2)列式表示:小明买大小笔记本共花 元.
(3)若小明从班长那里拿了300元,买了40本大小不同的两种笔记本(a=40),还找回55元给班长,那么小明买了大小笔记本各多少本?
(4)若这个班下次活动中,让小明刚好花400元购买这两种大小笔记本,并且购买的小笔记本数量x要小于60本,但还要超过30本(30<x<60),请列举小明有可能购买的方案,并说明理由.