题目内容
“康科迪亚”号大型游轮在地中海搁浅,派直升机与搜救船巡察情况,在距海面900米的A处测得搜救船在俯角为30°的海面C处,当直升机以140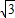 米/分的速度平行飞20分钟后到B处时测得搜救船在俯角为60°的海面D处,求搜救船平均速度.(保留三位有效数字;参考数据
米/分的速度平行飞20分钟后到B处时测得搜救船在俯角为60°的海面D处,求搜救船平均速度.(保留三位有效数字;参考数据 =1.414,
=1.414,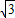 =1.732)
=1.732)
【答案】分析:首先分析图形,过点C作CE⊥AB,过B作BF⊥CD,根据题意构造直角三角形Rt△ACE与Rt△BDF.利用CE=DF构造方程,进而可解.
解答: 解:由题意得:AB=140
解:由题意得:AB=140 ×20=2800
×20=2800 (米)
(米)
过C作CE⊥AB于E,过B作BF⊥CD于F,则CE=BF=900米.
∵CE⊥AB,∠BAC=30°
∴在Rt△ACE中
tan30°=
∴
∴AE=900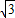 …(3分)
…(3分)
∴BE=AB-AE=2800 -900
-900 =1900
=1900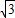
∵BF⊥CD,∠BDF=60°
∴在Rt△BFD中
tan60°=
∴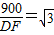
∴DF=300 …(5分)
…(5分)
∵AB∥CD,CE⊥AB,BF⊥CE.
∴四边形CEBF为矩形.
∴BE=CF=1900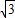
∴CD=1900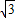 +300
+300 =2200
=2200 …(7分)
…(7分)
∴2200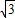 ÷20=110
÷20=110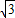 ≈191(米/分)
≈191(米/分)
答:搜救船的平均速度为191米/分.
点评:本题考查了解直角三角形的知识,要求学生借助仰角关系构造直角三角形,并结合图形利用三角函数解直角三角形.
解答:
 解:由题意得:AB=140
解:由题意得:AB=140 ×20=2800
×20=2800 (米)
(米) 过C作CE⊥AB于E,过B作BF⊥CD于F,则CE=BF=900米.
∵CE⊥AB,∠BAC=30°
∴在Rt△ACE中
tan30°=

∴

∴AE=900
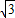 …(3分)
…(3分)∴BE=AB-AE=2800
 -900
-900 =1900
=1900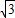
∵BF⊥CD,∠BDF=60°
∴在Rt△BFD中
tan60°=

∴
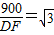
∴DF=300
 …(5分)
…(5分)∵AB∥CD,CE⊥AB,BF⊥CE.
∴四边形CEBF为矩形.
∴BE=CF=1900
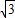
∴CD=1900
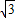 +300
+300 =2200
=2200 …(7分)
…(7分)∴2200
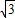 ÷20=110
÷20=110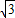 ≈191(米/分)
≈191(米/分) 答:搜救船的平均速度为191米/分.
点评:本题考查了解直角三角形的知识,要求学生借助仰角关系构造直角三角形,并结合图形利用三角函数解直角三角形.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
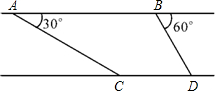 “康科迪亚”号大型游轮在地中海搁浅,派直升机与搜救船巡察情况,在距海面900米的A处测得搜救船在俯角为30°的海面C处,当直升机以140
“康科迪亚”号大型游轮在地中海搁浅,派直升机与搜救船巡察情况,在距海面900米的A处测得搜救船在俯角为30°的海面C处,当直升机以140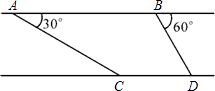 “康科迪亚”号大型游轮在地中海搁浅,派直升机与搜救船巡察情况,在距海面900米的A处测得搜救船在俯角为30°的海面C处,当直升机以140
“康科迪亚”号大型游轮在地中海搁浅,派直升机与搜救船巡察情况,在距海面900米的A处测得搜救船在俯角为30°的海面C处,当直升机以140 米/分的速度平行飞20分钟后到B处时测得搜救船在俯角为60°的海面D处,求搜救船平均速度.(保留三位有效数字;参考数据
米/分的速度平行飞20分钟后到B处时测得搜救船在俯角为60°的海面D处,求搜救船平均速度.(保留三位有效数字;参考数据 =1.414,
=1.414,
 米/分的速度平行飞20分钟后到B处时测得搜救船在俯角为60°的海面D处,求搜救船平均速度.(保留三位有效数字;参考数据
米/分的速度平行飞20分钟后到B处时测得搜救船在俯角为60°的海面D处,求搜救船平均速度.(保留三位有效数字;参考数据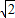 =1.414,
=1.414,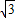 =1.732)
=1.732)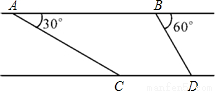
 米/分的速度平行飞20分钟后到B处时测得搜救船在俯角为60°的海面D处,求搜救船平均速度.(保留三位有效数字;参考数据
米/分的速度平行飞20分钟后到B处时测得搜救船在俯角为60°的海面D处,求搜救船平均速度.(保留三位有效数字;参考数据 =1.414,
=1.414, =1.732)
=1.732)