Question

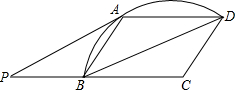如图，?ABCD的A、B、D三点在弧BD上，过A的直线PA交CB的延长线于P，若∠PAB=∠DBC，BC=2AB，?ABCD的面积为8，则△APB的面积为________．

Answer 1

1
分析：利用平行四边形的性质及相似三角形的判定定理可证昨△APB∽△BDC，再利用相似三角形的对应边成比例推出PB与BC间的等量关系，在△APB与△BCD中，高相等，面积之比等于底边PB与BC之比，而△BCD是?ABCD面积的一半，则△APB的面积可求．
解答：∵?ABCD
∴AB∥CD，AB=CD
∴∠PBA=∠C
∵∠PAB=∠DBC
∴△APB∽△BDC
∴AB：BC=PB：DC
∵BC=2AB
∴PB=DC=BC
∵BD是?ABCD的对角线
∴S_△BCD=S_?ABCD=×8=4
在△APB与△BCD中，分别以PB、BC为底边时，高相等
∴S_△APB=S_△BCD=1．
点评：本题主要考查了平行四边形的性质，相似三角形的判定定理及性质，三角形的面积的求法．