题目内容
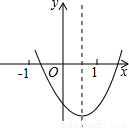
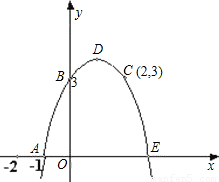
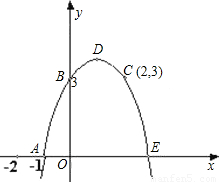
(2002•黄冈)已知:如图,抛物线c1经过A,B,C三点,顶点为D,且与x轴的另一个交点为E.(1)求抛物线c1解析式;
(2)求四边形ABDE的面积;
(3)△AOB与△BDE是否相似,如果相似,请予以证明;如果不相似,请说明理由;
(4)设抛物线c1的对称轴与x轴交于点F,另一条抛物线c2经过点E(抛物线c2与抛物线c1不重合),且顶点为M(a,b),对称轴与x轴相交于点G,且以M,G,E为顶点的三角形与以D,E,F为顶点的三角形全等,求a,b的值.(只需写出结果,不必写出解答过程)
【答案】分析:(1)根据图象可得出A、B、C三点的坐标,然后用待定系数法即可求出抛物线的解析式.
(2)由于四边形ABDE不是规则的四边形,因此可过D作DF⊥x轴于F,将四边形ABDE分成△AOB,梯形BOFD和△DFE三部分来求.
(3)可先根据坐标系中两点间的距离公式,分别求出AB、BE、DE、BD的长,然后看两三角形的线段是否对应成比例即可.
(4)要使两三角形全等,那么两直角三角形的两直角边应对应相等.
①当EF=EG=1,DF=MG=3,此时M点的坐标可能为(5,4),(5,-4),(1,-4).
②当EF=MG=1,DF=EG=3,此时M点的坐标可能是(7,1),(7,-1),(-1,1),(-1,-1).
综上所述可得出a、b的值.
解答:解:(1)设c1的解析式为y=ax2+bx+c,由图象可知:c1过A(-1,0),B(0,3),C(2,3)三点.
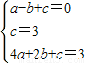
解得: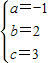
∴抛物线c1的解析式为y=-x2+2x+3.
(2)∵y=-x2+2x+3=-(x-1)2+4.
∴抛物线c1的顶点D的坐标为(1,4);
过D作DF⊥x轴于F,由图象可知:OA=1,OB=3,OF=1,DF=4;
令y=0,则-x2+2x+3=0,
解得x1=-1,x2=3
∴OE=3,则FE=2.
S△ABO= OA•OB=
OA•OB= ×1×3=
×1×3= ;
;
S△DFE= DF•FE=
DF•FE= ×4×2=4;
×4×2=4;
S梯形BOFD= (BO+DF)•OF=
(BO+DF)•OF= .
.
∴S四边形ABDE=S△AOB+S梯形BOFD+S△DFE=9(平方单位).
(3)如图,过B作BK⊥DF于K,则BK=OF=1.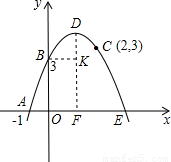
DK=DF-OB=4-3=1.
∴BD=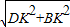 =
= ,
,
又DE=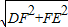 =2
=2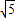 ;
;
AB=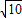 ,BE=3
,BE=3 ;
;
在△ABO和△BDE中,
AO=1,BO=3,AB=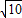 ;
;
BD=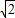 ,BE=3
,BE=3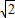 ,DE=2
,DE=2 .
.
∵ =
=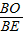 =
=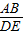 =
=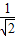
∴△AOB∽△DBE.
(4)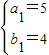 ,
,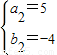 ,
,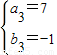 ,
,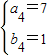 ,
,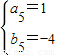 ,
, ,
,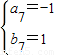 .
.
点评:本题着重考查了待定系数法求二次函数解析式、三角形相似、图形面积的求法等知识点,综合性强,考查学生分类讨论,数形结合的数学思想方法.
(2)由于四边形ABDE不是规则的四边形,因此可过D作DF⊥x轴于F,将四边形ABDE分成△AOB,梯形BOFD和△DFE三部分来求.
(3)可先根据坐标系中两点间的距离公式,分别求出AB、BE、DE、BD的长,然后看两三角形的线段是否对应成比例即可.
(4)要使两三角形全等,那么两直角三角形的两直角边应对应相等.
①当EF=EG=1,DF=MG=3,此时M点的坐标可能为(5,4),(5,-4),(1,-4).
②当EF=MG=1,DF=EG=3,此时M点的坐标可能是(7,1),(7,-1),(-1,1),(-1,-1).
综上所述可得出a、b的值.
解答:解:(1)设c1的解析式为y=ax2+bx+c,由图象可知:c1过A(-1,0),B(0,3),C(2,3)三点.
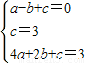
解得:
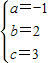
∴抛物线c1的解析式为y=-x2+2x+3.

(2)∵y=-x2+2x+3=-(x-1)2+4.
∴抛物线c1的顶点D的坐标为(1,4);
过D作DF⊥x轴于F,由图象可知:OA=1,OB=3,OF=1,DF=4;
令y=0,则-x2+2x+3=0,
解得x1=-1,x2=3
∴OE=3,则FE=2.
S△ABO=
 OA•OB=
OA•OB= ×1×3=
×1×3= ;
;S△DFE=
 DF•FE=
DF•FE= ×4×2=4;
×4×2=4;S梯形BOFD=
 (BO+DF)•OF=
(BO+DF)•OF= .
.∴S四边形ABDE=S△AOB+S梯形BOFD+S△DFE=9(平方单位).
(3)如图,过B作BK⊥DF于K,则BK=OF=1.

DK=DF-OB=4-3=1.
∴BD=
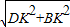 =
= ,
,又DE=
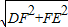 =2
=2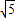 ;
;AB=
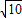 ,BE=3
,BE=3 ;
;在△ABO和△BDE中,
AO=1,BO=3,AB=
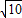 ;
;BD=
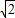 ,BE=3
,BE=3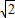 ,DE=2
,DE=2 .
.∵
 =
=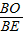 =
=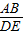 =
=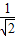
∴△AOB∽△DBE.
(4)
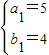 ,
,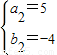 ,
,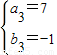 ,
,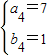 ,
,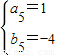 ,
, ,
,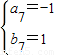 .
.点评:本题着重考查了待定系数法求二次函数解析式、三角形相似、图形面积的求法等知识点,综合性强,考查学生分类讨论,数形结合的数学思想方法.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
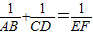 成立(不要求考生证明).
成立(不要求考生证明).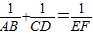 还成立吗?如果成立,请给出证明;如果不成立,请说明理由;
还成立吗?如果成立,请给出证明;如果不成立,请说明理由;