题目内容
【题目】学农期间我们完成了每日一题，进一步研究了角的平分线. 工人师傅常用角尺平分一个任意角. 作法如下：
如图，∠AOB 是一个任意角，在边 OA、OB 上分别取 OM=ON， 移动角尺，使角尺两边相同的刻度分别与 M、N 重合. 过角尺顶点 C 的射线 OC 便是∠AOB 的平分线. 我们发现利用 SSS 证明两个三角形全等，从而证明∠AOC=∠BOC.
学习了轴对称的知识后，我们知道角是轴对称图形，角平分线 所在直线就是它的对称轴，爱动脑筋的小慧同学利用轴对称图形的性质发现了一种画角平分线的方法.
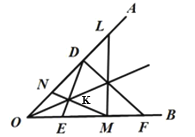
方法如下：如图 1，将两个全等的三角形纸片△DEF 和△MNL 的一组对应边分别与∠AOB 的一边共线，同时这条边所对顶点落在∠AOB 的另一条边上，则△DEF 和△MNL 的另一组对应边的交点 P 在∠AOB 的平分线上.
（1）小慧的做法正确吗？说明理由：
小旭说：利用轴对称的性质，我只用刻度尺就可以画角平分线.（提示：刻度尺可以度量出相等的线段）
（2）请你和小旭一样，只用刻度尺画出图 2 中∠QRS 的角平分线.（保留作图痕迹，不写作法）
【答案】（1）正确，证明见解析（2）图见解析.
【解析】
（1）说法正确，可通过用AAS证明三角形OED与三角形OME全等得到ON=OE，OD=OM，∠ODE=∠ONM，再根据DO-ON=OM-OE，得到DN=ME，再根据AAS证明三角形NKD与三角形EKM全等，得到NK=EK,再根据SAS证明三角形ONK与三角形OEK全等，从而得到对应角∠NOK=∠EOK，即可证明角平分线.
（2）根据（1）可知，作三角形RAD与三角形RBC全等，过R点作与BC与AD的交点的射线即为角平分线.
（1）正确.理由如下
∵
∴∠DEF=∠MNL，DE=NM
∴180°-∠DEF=180°-∠MNL
即∠OED=∠ONM
在三角形OED与三角形ONM中
∴
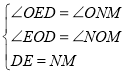
(AAS)
∴ON=OE，OD=OM，∠ODE=∠OMN
∴DO-ON=OM-OE
即DN=ME
在三角形NKD与三角形EKM中
∴
(AAS)
∴NK=EK
在三角形ONK与三角形OEK中
∴
(SAS)
∴∠NOK=∠EOK
即OK为∠LOF 的角平分线.
（2）
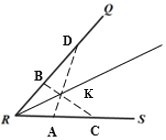
如图量RA=RA，RQ=RC，连接AD=BC.
则在三角形RAD与三角形RBC中
∴
（SAS）
∴∠RDA=∠RCB
在三角形BDK与三角形ACK中
∴
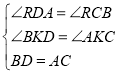
（AAS）
∴BK=AK
在三角形RBK与三角形RAK中
∴
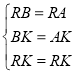
(SSS)
∴∠BRK=∠ARK
故RK为角平分线.
