题目内容
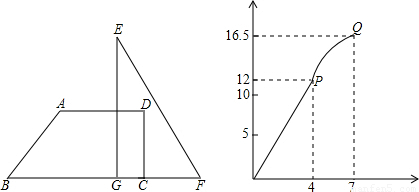
(2009•莲都区模拟)如图,在梯形ABCD中,AD∥BC,∠BCD=Rt∠,∠B=45°小宇用一块三角板EGF,使直角边EG与CD重合,点G与点C重合,直角边EG沿着CB从点C往点B平移,当点G运动到点B时,平移就结束.设CG的长度为xcm,梯形ABCD被直角边EG扫过的面积为ycm2,y与x的图象如图2所示,其中OP是线段,曲线PQ是抛物线的一部分,抛物线的顶点是Q(7, ).
).
(1)直接写出BC、AD、CD的长度;
(2)求出y与x之间的函数关系式,并写出自变量的范围;
(3)探究:三角板直角边EG在运动过程中,是否存在这样的点G,使得以A、D、G为顶点的三角形为等腰三角形?如果存在,求出x的值,如果不存在,请说明理由.
【答案】分析:(1)当运动到点A时,面积开始不是均匀变化,那么AD=CG=4,根据面积为12可得CD为3,等于7时结束,那么BC=7;
(2)当x≤4时,可设函数解析式为y=kx,把(4,12)代入即可求解,当4<x≤7时,利用顶点式即可求得相应函数解析式;
(3)A、D、G为顶点的三角形为等腰三角形时应分情况进行探讨.当AD=DG时,有1种情况,当AG=AD时,有2种情况,当AG=DG时,有一种情况.
解答: 解:(1)易得四边形AG′CD为矩形,
解:(1)易得四边形AG′CD为矩形,
∴AD=G′C=4,
∴CD=12÷4=3,
当x=7时,运动结束,
∴BC=x=7;
(2)当0≤x≤4时,
设函数解析式为y=kx,
∴4k=12,
k=3,
∴y=3x,
当4<x≤7时,
设函数解析式为y=a(x-7)2+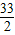 ,
,
∴12=9a+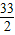 ,
,
解得a=- ,
,
∴y=- (x-7)2+
(x-7)2+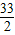 ,
,
∴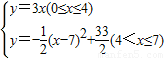 ;
;
(3)AD=AG时,
GG′=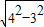 =
=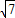 ,
,
所以x=4+ ,或者x=4-
,或者x=4-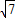 .
.
同理可得AD=DG,点D为两腰的交点时,
x=GG′=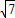 ;
;
当AG=DG时,
x= AD=2.
AD=2.
点评:抛物线上有顶点坐标,所求的抛物线解析式应设为顶点式求解比较简便;三角形为等腰三角形,应分不同顶点为两腰的交点进行分类讨论.
(2)当x≤4时,可设函数解析式为y=kx,把(4,12)代入即可求解,当4<x≤7时,利用顶点式即可求得相应函数解析式;
(3)A、D、G为顶点的三角形为等腰三角形时应分情况进行探讨.当AD=DG时,有1种情况,当AG=AD时,有2种情况,当AG=DG时,有一种情况.
解答:
 解:(1)易得四边形AG′CD为矩形,
解:(1)易得四边形AG′CD为矩形,∴AD=G′C=4,
∴CD=12÷4=3,
当x=7时,运动结束,
∴BC=x=7;
(2)当0≤x≤4时,
设函数解析式为y=kx,
∴4k=12,
k=3,
∴y=3x,
当4<x≤7时,
设函数解析式为y=a(x-7)2+
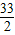 ,
,∴12=9a+
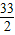 ,
,解得a=-
 ,
,∴y=-
 (x-7)2+
(x-7)2+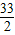 ,
,∴
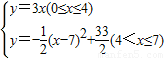 ;
;(3)AD=AG时,
GG′=
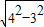 =
=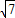 ,
,所以x=4+
 ,或者x=4-
,或者x=4-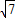 .
.同理可得AD=DG,点D为两腰的交点时,
x=GG′=
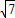 ;
;当AG=DG时,
x=
 AD=2.
AD=2.点评:抛物线上有顶点坐标,所求的抛物线解析式应设为顶点式求解比较简便;三角形为等腰三角形,应分不同顶点为两腰的交点进行分类讨论.

练习册系列答案
相关题目