题目内容
已知某种水果的批发单价与批发量的函数关系如图(1)所示.
(1)请说明图中①、②两段函数图象的实际意义;

(2)写出批发该种水果的资金金额w(元)与批发量m(kg)之间的函数关系式;在下图的坐标系中画出该函数图象;指出金额在什么范围内,以同样的资金可以批发到较多数量的该种水果;

(3)经调查,某经销商销售该种水果的日最高销量与零售价之间的函数关系如图(2)所示,该经销商拟每日售出60kg以上该种水果,且当日零售价不变,请你帮助该经销商设计进货和销售的方案,使得当日获得的利润最大.

(1)请说明图中①、②两段函数图象的实际意义;

(2)写出批发该种水果的资金金额w(元)与批发量m(kg)之间的函数关系式;在下图的坐标系中画出该函数图象;指出金额在什么范围内,以同样的资金可以批发到较多数量的该种水果;

(3)经调查,某经销商销售该种水果的日最高销量与零售价之间的函数关系如图(2)所示,该经销商拟每日售出60kg以上该种水果,且当日零售价不变,请你帮助该经销商设计进货和销售的方案,使得当日获得的利润最大.

(1)解:图①表示批发量不少于20kg且不多于60kg的该种水果,可按5元/kg批发;
图②表示批发量高于60kg的该种水果,可按4元/kg批发.
(2)解:由题意得: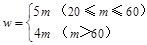 ,函数图象如图所示.
,函数图象如图所示.
由图可知资金金额满足240<w≤300时,以同样的资金可批发到较多数量的该种水果.
(3)解法一:设当日零售价为x元,由图可得日最高销量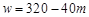
当m>60时,x<6.5,由题意,销售利润为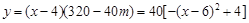
当x=6时,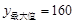 ,此时m=80即经销商应批发80kg该种水果,日零售价定为6元/kg,当日可获最大利润160元.
,此时m=80即经销商应批发80kg该种水果,日零售价定为6元/kg,当日可获最大利润160元.
解法二:设日最高销售量为xkg(x>60)
则由图②日零售价p满足: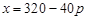 ,于是
,于是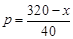
销售利润 当x=80时,
当x=80时,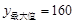 ,
,
此时p=6即经销商应批发80kg该种水果,日零售价定为6元/kg,当日可获得最大利润160元.
图②表示批发量高于60kg的该种水果,可按4元/kg批发.
(2)解:由题意得:
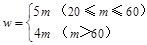 ,函数图象如图所示.
,函数图象如图所示.由图可知资金金额满足240<w≤300时,以同样的资金可批发到较多数量的该种水果.
(3)解法一:设当日零售价为x元,由图可得日最高销量
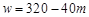
当m>60时,x<6.5,由题意,销售利润为
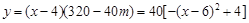
当x=6时,
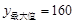 ,此时m=80即经销商应批发80kg该种水果,日零售价定为6元/kg,当日可获最大利润160元.
,此时m=80即经销商应批发80kg该种水果,日零售价定为6元/kg,当日可获最大利润160元. 解法二:设日最高销售量为xkg(x>60)
则由图②日零售价p满足:
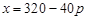 ,于是
,于是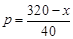
销售利润
 当x=80时,
当x=80时,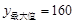 ,
,此时p=6即经销商应批发80kg该种水果,日零售价定为6元/kg,当日可获得最大利润160元.
(1)根据图象特征即可得到结果;
(2)先作出图象,根据图象特征即可得到结果;
根据销售利润与销售价、销售量的关系列出二次函数关系式,根据二次函数解析式的顶点式即可求出最大利润。
(2)先作出图象,根据图象特征即可得到结果;
根据销售利润与销售价、销售量的关系列出二次函数关系式,根据二次函数解析式的顶点式即可求出最大利润。

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
 =
= 的自变量
的自变量 的取值范围是 。
的取值范围是 。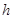 ,注水时间为
,注水时间为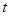 ,则
,则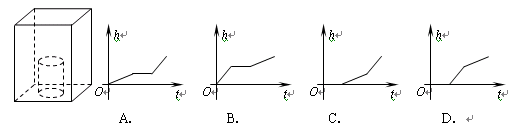
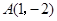 关于
关于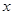 轴对称的点的坐标是 ;点
轴对称的点的坐标是 ;点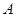 关于原点对称的点的坐标是 .
关于原点对称的点的坐标是 . ,DE的延长线交CB的延长线于点F,设CF=
,DE的延长线交CB的延长线于点F,设CF=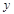 ,则下列图象能正确反映
,则下列图象能正确反映



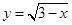 +
+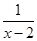 中自变量x的取值范围是( )
中自变量x的取值范围是( )

 且
且
 且
且