题目内容
 有蓝、黑两种颜色的水性笔各一支(分别记为蓝色笔为A,黑色笔为B)和与之颜色相同的匹配笔帽(分别记蓝色笔帽为a,黑色笔帽为b)(如本题图所示)放在桌子上.
有蓝、黑两种颜色的水性笔各一支(分别记为蓝色笔为A,黑色笔为B)和与之颜色相同的匹配笔帽(分别记蓝色笔帽为a,黑色笔帽为b)(如本题图所示)放在桌子上.
(1)若从水性笔中随机取一个,再从笔帽中随机取一个,求恰好颜色匹配的概率.
(2)若从水性笔和笔帽中随机取出两个,用树形图法或列表法,求恰好颜色匹配的概率.
解:(1)从水性笔中随机抽取一个,再从笔帽中随机取一个,有Aa,Ab,Ba,Bb四种情况.
恰好颜色匹配的有Aa,Bb两种情况,
∴P(恰好匹配)= ;
;
(2)用树形图法表示:
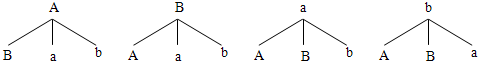
所有可能的结果AB Aa Ab BA Ba Bb aA aB ab bA bB ba
可见,从水性笔和笔帽中随机取两个,共有12种不同的情况.
其中恰好匹配的有4种,分别是Aa,Bb,aA,bB,
P(恰好匹配)= =
= .
.
分析:(1)列举出所有情况,看颜色匹配的情况数占总情况数的多少即可;
(2)列举出所有情况,看颜色匹配的情况数占总情况数的多少即可.
点评:考查概率的求法;用到的知识点为:概率=所求情况数与总情况数之比;理解清楚题意,得到每次拿出的情况数是解决本题的关键.
恰好颜色匹配的有Aa,Bb两种情况,
∴P(恰好匹配)=
 ;
;(2)用树形图法表示:
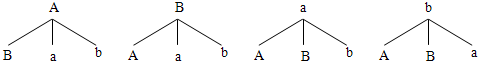
所有可能的结果AB Aa Ab BA Ba Bb aA aB ab bA bB ba
可见,从水性笔和笔帽中随机取两个,共有12种不同的情况.
其中恰好匹配的有4种,分别是Aa,Bb,aA,bB,
P(恰好匹配)=
 =
= .
.分析:(1)列举出所有情况,看颜色匹配的情况数占总情况数的多少即可;
(2)列举出所有情况,看颜色匹配的情况数占总情况数的多少即可.
点评:考查概率的求法;用到的知识点为:概率=所求情况数与总情况数之比;理解清楚题意,得到每次拿出的情况数是解决本题的关键.

练习册系列答案
相关题目
 有蓝、黑两种颜色的水性笔各一支(分别记为蓝色笔为A,黑色笔为B)和与之颜色相同的匹配笔帽(分别记蓝色笔帽为a,黑色笔帽为b)(如本题图所示)放在桌子上.
有蓝、黑两种颜色的水性笔各一支(分别记为蓝色笔为A,黑色笔为B)和与之颜色相同的匹配笔帽(分别记蓝色笔帽为a,黑色笔帽为b)(如本题图所示)放在桌子上.