��Ŀ����
�����㣨1��1����ֱ��l�� �뷴��������G1:
�뷴��������G1: ��ͼ���ڵ�
��ͼ���ڵ� ��B��b��-1������y�ύ�ڵ�D��
��B��b��-1������y�ύ�ڵ�D��
��1����ֱ��l��Ӧ�ĺ�������ʽ������������G1�ı���ʽ��
��2������������G2:: ��
��
������E�ڵ�һ�����ڣ����ڷ���������G2��ͼ���ϣ���EA=EB���ҡ�AEB�����Ϊ8�����E�����꼰tֵ��
�ڷ���������G2��ͼ����ֱ��l������������M��N����M�ڵ�N����ࣩ���� ��ֱ��д��t��ȡֵ��Χ��
��ֱ��д��t��ȡֵ��Χ��
��1�� ,
, ;��2����E (
;��2����E ( ),9; ��
),9; ��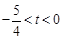 ��
�� .
.
���������������1����ֱ��l: ����
���� ���������
��������� ���Ӷ��õ�ֱ��l��Ӧ�ĺ�������ʽ;��ֱ��l�뷴��������G1:
���Ӷ��õ�ֱ��l��Ӧ�ĺ�������ʽ;��ֱ��l�뷴��������G1: ��ͼ���ڵ�
��ͼ���ڵ� ��B��b ��-1�����ֱ����ɵ�
��B��b ��-1�����ֱ����ɵ� ���Ӷ��õ�����������G1�ı���ʽ.
���Ӷ��õ�����������G1�ı���ʽ.
��2���ٸ�����֪�ɵá�AEB �ǵ���ֱ��������,�Ӷ���õ�E�����꼰tֵ��
�ڷ�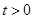 ��
�� ����������ۼ���.
����������ۼ���.
�����������1����ֱ��l: ����
���� ����
���� .
.
��ֱ��l��Ӧ�ĺ�������ʽ ��
��
��ֱ��l�뷴��������G1: ��ͼ���ڵ�
��ͼ���ڵ� ��B��b ��-1����
��B��b ��-1����
�� ����
���� ��B��3��-1������
��B��3��-1������ ��
��
�෴��������G1��������ʽΪ ����֪
����֪
��2���١�EA=EB�� ��B��3��-1�������E��ֱ��y=x�ϣ�
��B��3��-1�������E��ֱ��y=x�ϣ�
�ߡ�AEB�����Ϊ8�� ����
���� ��
��
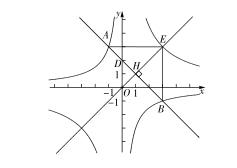
���AEB �ǵ���ֱ�������Σ���E ( ).
). .
.
�ڷ����������
��������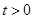 ʱ����
ʱ���� ��
��
�������� ʱ����
ʱ����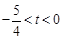 ��
��
���ϣ���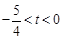 ��
�� ʱ������������
ʱ������������ ��ͼ����ֱ��l������������M��N����
��ͼ����ֱ��l������������M��N���� ��
��
���㣺1.������������һ�κ�����������;2.�����ϵ�������뷽�̵Ĺ�ϵ;3������ֱ�������ε��ж�������;3.����˼���Ӧ��.

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д��ţ�1������ѧ��ȤС�龭���г����飬������ij����Ʒ�ڵ�x��1��x��90������ۼ����������������Ϣ���±���
| ʱ��x���죩 | 1��x��50 | 50��x��90 |
| �ۼۣ�Ԫ/���� | x��40 | 90 |
| ÿ������������ | 200��2x | |
��֪����Ʒ�Ľ���Ϊÿ��30Ԫ�������۸���Ʒ��ÿ������ΪyԪ[
��1�����y��x�ĺ�����ϵʽ��
��2�������۸���Ʒ�ڼ���ʱ�������������������������Ƕ��٣�
��3������Ʒ�����۹����У����ж�����ÿ������������4800Ԫ����ֱ��д�����.
 ��m��0��x��0����ͼ���ڵ�һ��������ֱ��L������һ������ʱ����m��ȡֵ��Χ��
��m��0��x��0����ͼ���ڵ�һ��������ֱ��L������һ������ʱ����m��ȡֵ��Χ�� ʱ����m��ֵ��
ʱ����m��ֵ��

 ��Ԫ����ɹ���
��Ԫ����ɹ��� ���֮��Ĺ�ϵ��ͼ���Ҳɹ����۲�����4Ԫ/�
���֮��Ĺ�ϵ��ͼ���Ҳɹ����۲�����4Ԫ/�
 ����B��2����4����һ�κ���
����B��2����4����һ�κ��� ��ͼ��ͷ���������
��ͼ��ͷ��������� ��ͼ����������㡣
��ͼ����������㡣 ��Ľ���C�����꼰��AOB�������
��Ľ���C�����꼰��AOB������� �Ľ⣨��ֱ��д���𰸣���
�Ľ⣨��ֱ��д���𰸣��� �Ľ⼯����ֱ��д���𰸣���
�Ľ⼯����ֱ��д���𰸣���
 ��Ԫ�����л�����A�ͳ���
��Ԫ�����л�����A�ͳ���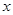 �ڣ���д��
�ڣ���д�� ��ֱ�ߵĽ���A��B���ڸ���ϣ�����������ֱ������ϵ��O������ԭ�㣩������������⣺
��ֱ�ߵĽ���A��B���ڸ���ϣ�����������ֱ������ϵ��O������ԭ�㣩������������⣺