题目内容
如图，已知△ABC为等腰直角三角形，D为斜边BC的中点，经过点A、D的⊙O与边AB、AC、BC分别相交于点E、F、M．对于如下五个结论：①∠FMC=45°；②AE+AF=AB；③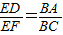
；④2BM2=BE•BA；⑤四边形AEMF为矩形．其中正确结论的个数是（ ）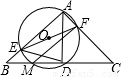
A．2个
B．3个
C．4个
D．5个
【答案】分析：根据等腰直角三角形的性质和直径所对的圆周角是90°，90°圆周角所对的弦是直径逐项判断后利用排除法求解．
解答：解：连接AM，根据等腰三角形的三线合一，得AD⊥BC，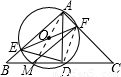
再根据90°的圆周角所对的弦是直径，得EF、AM是直径，
根据对角线相等且互相平分的四边形是矩形，得四边形AEMF是矩形，
∴①根据等腰直角三角形ABC的底角是45°，易得∠FMC=45°，正确；
②根据矩形和等腰直角三角形的性质，得AE+AF=AB，正确；
③连接FD，可以证明△EDF是等腰直角三角形，则③中左右两边的比都是等腰直角三角形的直角边和斜边的比，正确；
④根据BM=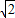
BE，得左边=4BE2，故需证明AB=4BE，根据已知条件它们之间不一定有这种关系，错误；
⑤正确．
所以①②③⑤共4个正确．故选C．
点评：此题注意熟练运用圆周角定理的推论发现矩形和等腰直角三角形．
解答：解：连接AM，根据等腰三角形的三线合一，得AD⊥BC，
再根据90°的圆周角所对的弦是直径，得EF、AM是直径，
根据对角线相等且互相平分的四边形是矩形，得四边形AEMF是矩形，
∴①根据等腰直角三角形ABC的底角是45°，易得∠FMC=45°，正确；
②根据矩形和等腰直角三角形的性质，得AE+AF=AB，正确；
③连接FD，可以证明△EDF是等腰直角三角形，则③中左右两边的比都是等腰直角三角形的直角边和斜边的比，正确；
④根据BM=
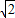BE，得左边=4BE2，故需证明AB=4BE，根据已知条件它们之间不一定有这种关系，错误；⑤正确．
所以①②③⑤共4个正确．故选C．
点评：此题注意熟练运用圆周角定理的推论发现矩形和等腰直角三角形．
练习册系列答案
相关题目
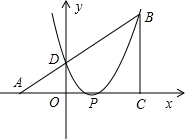，m）（m＞0），线段AB与y轴相交于点D，以P（1，0）为顶点的二次函数图象经过点B、D．
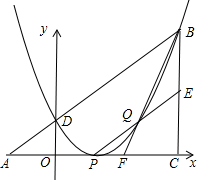如图，已知△ABC为直角三角形，∠ACB=90°，AC=BC，点A、C在x轴上，点B坐标为（3，m）（m＞0），线段AB与y轴相交于点D，以P（1，0）为顶点的抛物线过点B、D．
25、如图，已知△ABC为等边三角形，D、F分别为BC、AB边上的点，CD=BF，以AD为边作等边△ADE．
如图，已知△ABC为等边三角形，D，E，F分别在边BC，CA，AB上，且△DEF也是等边三角形，除已知相等的边以外，请你猜想还有哪些相等线段，并证明你的猜想是正确的．
如图，已知△ABC为等边三角形，点D．E分别在BC．AC边上，且AE=CD，AD与BE相交于点F．