题目内容
如图,已知△ABC为直角三角形,∠ACB=90°,AC=BC,点A、C在x轴上,点B坐标为(3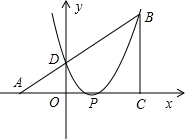 ,m)(m>0),线段AB与y轴相交于点D,以P(1,0)为顶点的二次函数图象经过点B、D.
,m)(m>0),线段AB与y轴相交于点D,以P(1,0)为顶点的二次函数图象经过点B、D.(1)用m表示点A、D的坐标;
(2)求这个二次函数的解析式;
(3)点Q为二次函数图象上点P至点B之间的一点,且点Q到△ABC边BC、AC的距离相等,连接PQ、BQ,求四边形ABQP的面积.
分析:(1)由△ABC为直角三角形,∠ACB=90°,AC=BC,可得出AO=0D,由点B坐标为(3,m)得出AC的长度和OC的长,从而得出点A、D的坐标;
(2)由二次函数图象的顶点坐标为P(1,0),且过点B、D,代入y=k(x-1)2,求出即可;
(3)根据四边形ABQP的面积=△ABC的面积-(△CBQ的面积+△CPQ的面积)求出即可.
(2)由二次函数图象的顶点坐标为P(1,0),且过点B、D,代入y=k(x-1)2,求出即可;
(3)根据四边形ABQP的面积=△ABC的面积-(△CBQ的面积+△CPQ的面积)求出即可.
解答:解:(1)∵点B坐标为(3,m)(m>0),
∴OC=3,BC=m.
∵AC=BC,
∴AC=m,
∴点A坐标为(3-m,0),
由题意得:AO=OD,
∴点D坐标为(0,m-3);
(2)设以P(1,0)为顶点的抛物线的解析式为y=k(x-1)2(k≠0),
∵抛物线过点B、D,
∴
,
解得:
,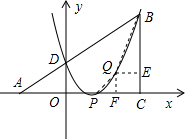
所以二次函数的解析式为y=(x-1)2,
即:y=x2-2x+1;
(3)设点Q的坐标为(x,y),显然1<x<3,y>0.
∵点Q到△ABC边BC、AC的距离相等,
∴QE=FQ=y,
∵CO=3,∴x+y=3,y=3-x,即x2-2x+1=3-x,
整理得x2-x-2=0.解得x=2,x=-1(舍去),
所以y=1,点Q的坐标为(2,1),点Q到边AC、BC的距离都等于1.
连接CQ,
四边形ABQP的面积=△ABC的面积-四边形CBQP的面积,
=△ABC的面积-(△CBQ的面积+△CPQ的面积),
=
×4×4-(
×4×1+
×2×1)=5.
∴OC=3,BC=m.
∵AC=BC,
∴AC=m,
∴点A坐标为(3-m,0),
由题意得:AO=OD,
∴点D坐标为(0,m-3);
(2)设以P(1,0)为顶点的抛物线的解析式为y=k(x-1)2(k≠0),
∵抛物线过点B、D,
∴
|
解得:
|

所以二次函数的解析式为y=(x-1)2,
即:y=x2-2x+1;
(3)设点Q的坐标为(x,y),显然1<x<3,y>0.
∵点Q到△ABC边BC、AC的距离相等,
∴QE=FQ=y,
∵CO=3,∴x+y=3,y=3-x,即x2-2x+1=3-x,
整理得x2-x-2=0.解得x=2,x=-1(舍去),
所以y=1,点Q的坐标为(2,1),点Q到边AC、BC的距离都等于1.
连接CQ,
四边形ABQP的面积=△ABC的面积-四边形CBQP的面积,
=△ABC的面积-(△CBQ的面积+△CPQ的面积),
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:此题主要考查了二次函数解析式的求法和一般四边形面积求法,将四边形分割成几个三角形和差的形式是解决问题的关键.

练习册系列答案
相关题目
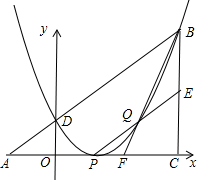 如图,已知△ABC为直角三角形,∠ACB=90°,AC=BC,点A、C在x轴上,点B坐标为(3,m)(m>0),线段AB与y轴相交于点D,以P(1,0)为顶点的抛物线过点B、D.
如图,已知△ABC为直角三角形,∠ACB=90°,AC=BC,点A、C在x轴上,点B坐标为(3,m)(m>0),线段AB与y轴相交于点D,以P(1,0)为顶点的抛物线过点B、D. 25、如图,已知△ABC为等边三角形,D、F分别为BC、AB边上的点,CD=BF,以AD为边作等边△ADE.
25、如图,已知△ABC为等边三角形,D、F分别为BC、AB边上的点,CD=BF,以AD为边作等边△ADE. 如图,已知△ABC为等边三角形,D,E,F分别在边BC,CA,AB上,且△DEF也是等边三角形,除已知相等的边以外,请你猜想还有哪些相等线段,并证明你的猜想是正确的.
如图,已知△ABC为等边三角形,D,E,F分别在边BC,CA,AB上,且△DEF也是等边三角形,除已知相等的边以外,请你猜想还有哪些相等线段,并证明你的猜想是正确的. 如图,已知△ABC为等边三角形,点D.E分别在BC.AC边上,且AE=CD,AD与BE相交于点F.
如图,已知△ABC为等边三角形,点D.E分别在BC.AC边上,且AE=CD,AD与BE相交于点F.