题目内容
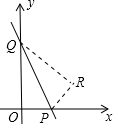如图，直线y=-2x+6与x轴、y轴分别交于P、Q两点，把△POQ沿PQ翻折，点O落在R处，则点R的坐标是分析：先设出R点的坐标，再由一次函数的性质分别求出P、Q两点的坐标，再根据图形翻折不变性的性质可得到OP=RP，OQ=RQ，利用两点间的距离公式即可求解．
解答：解：设R（a，b），
∵直线y=-2x+6与x轴、y轴分别交于P、Q两点，
∴令x=0，则y=6，令y=0，则x=3，
∴P（3，0），Q（0，6），
∴OP=3，OQ=6，
∵△PQR是沿QP翻折而成的，
∴RP=OP，OQ=QR，
∴
=OP=3，
=OQ=6，
解得a=
，b=
，
故R点的坐标为：（
，
）．
故答案为：（
，
）．
∵直线y=-2x+6与x轴、y轴分别交于P、Q两点，
∴令x=0，则y=6，令y=0，则x=3，
∴P（3，0），Q（0，6），
∴OP=3，OQ=6，
∵△PQR是沿QP翻折而成的，
∴RP=OP，OQ=QR，
∴
| (a-3)2+b2 |
| a2+(6-b)2 |
解得a=
| 24 |
| 5 |
| 12 |
| 5 |
故R点的坐标为：（
| 24 |
| 5 |
| 12 |
| 5 |
故答案为：（
| 24 |
| 5 |
| 12 |
| 5 |
点评：本题考查的值图形翻折变换的性质及两点间的距离公式，熟知图形翻折变换的性质是解答此题的关键．
练习册系列答案
相关题目
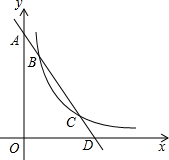如图，直线y=-2x+b与y轴交于点A，与x轴交于点D，与双曲线
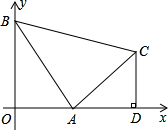腰直角△ABC，∠BAC=90°，过C作CD⊥x轴，垂足为D．
轴分别交于点C、D．直线EB交x轴于点F．
如图，直线y=-2x+8与两坐标轴分别交于P，Q两点，在线段PQ上有一点A，过点A分别作两坐标轴的垂线，垂足分别为B、C．