题目内容
【题目】已知,如图,直线AB、CD、EF都经过点O,且AB⊥CD,OG平分∠BOE,如果∠EOG= ![]() ∠AOE,求∠EOG和∠DOF的度数.
∠AOE,求∠EOG和∠DOF的度数. 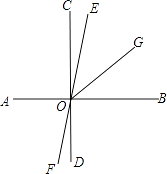
【答案】解:∵OG平分∠BOE,
∴∠EOG=∠BOG,
设∠AOE=x°,
∴∠EOG=∠GOB= ![]() x°,
x°,
∴x+ ![]() x+
x+ ![]() x=180,
x=180,
解得:x=100,
∴∠EOG=100°× ![]() =40°,
=40°,
∵AB⊥CD,
∴∠BOC=90°,
∴∠DOF=∠COE=90°﹣40°﹣40°=10°
【解析】首先根据角平分线的性质可得∠EOG=∠BOG,设∠AOE=x°,进而得到∠EOG=∠GOB= ![]() x°,再根据平角为180°可得x+
x°,再根据平角为180°可得x+ ![]() x+
x+ ![]() x=180,解出x可得∠EOG,进而可得∠DOF的度数.
x=180,解出x可得∠EOG,进而可得∠DOF的度数.
【考点精析】根据题目的已知条件,利用角的平分线和对顶角和邻补角的相关知识可以得到问题的答案,需要掌握从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线;两直线相交形成的四个角中,每一个角的邻补角有两个,而对顶角只有一个.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目