题目内容
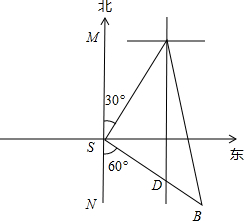
两座灯塔A和B与海岸观察站S的距离相等，A在S北偏东30°方向，B在S的南偏东60°方向，则灯塔B在灯塔A的______方向．
由题意得∠MSA=30°，∠NSB=60°，
∴∠ASB=180°-30°-60°=90°，
∵AS=BS，
∴∠SAB=45°．
∵MN∥AD，
∴∠SAD=∠MSA=30°，
∴∠BAD=∠SAB-∠SAD=45°-30°=15°．
∴灯塔B在灯塔A的南偏东15°．
故答案为：南偏东15°．
∴∠ASB=180°-30°-60°=90°，
∵AS=BS，
∴∠SAB=45°．
∵MN∥AD，
∴∠SAD=∠MSA=30°，
∴∠BAD=∠SAB-∠SAD=45°-30°=15°．
∴灯塔B在灯塔A的南偏东15°．
故答案为：南偏东15°．
练习册系列答案
优翼小帮手同步口算系列答案
相关题目
