题目内容
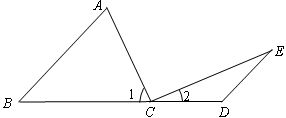
 如图,点A在线段ED上,AC=CD,BC=CE,∠1=∠2,如果AB=7,AD=5,那么AE=________.
如图,点A在线段ED上,AC=CD,BC=CE,∠1=∠2,如果AB=7,AD=5,那么AE=________.
2
分析:由于∠1=∠2,利用等量相加和相等可得∠ACB=∠DCE,而AC=CD,BC=CE,根据SAS易证△ACB≌△DCE,于是DE=7,结合AD=5,进而可求AE.
解答:证明: ∵∠1=∠2,
∵∠1=∠2,
∴∠1+∠ACE=∠2+∠ACE,
即∠ACB=∠DCE,
又∵AC=CD,BC=CE,
∴△ACB≌△DCE,
∴DE=AB=7,
又AD=5,
∴AE=DE-AD=7-5=2.
故答案是2.
点评:本题考查了全等三角形的判定和性质,解题的关键是证明△ACB≌△DCE.
分析:由于∠1=∠2,利用等量相加和相等可得∠ACB=∠DCE,而AC=CD,BC=CE,根据SAS易证△ACB≌△DCE,于是DE=7,结合AD=5,进而可求AE.
解答:证明:
 ∵∠1=∠2,
∵∠1=∠2,∴∠1+∠ACE=∠2+∠ACE,
即∠ACB=∠DCE,
又∵AC=CD,BC=CE,
∴△ACB≌△DCE,
∴DE=AB=7,
又AD=5,
∴AE=DE-AD=7-5=2.
故答案是2.
点评:本题考查了全等三角形的判定和性质,解题的关键是证明△ACB≌△DCE.

练习册系列答案
相关题目

 如图,点A在线段ED上,AC=CD,BC=CE,∠1=∠2,如果AB=7,AD=5,那么AE=
如图,点A在线段ED上,AC=CD,BC=CE,∠1=∠2,如果AB=7,AD=5,那么AE=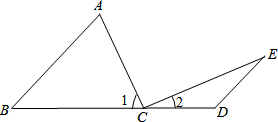 如图:点C在线段BD上,AB∥ED,∠A=∠1,∠E=∠2.
如图:点C在线段BD上,AB∥ED,∠A=∠1,∠E=∠2.