题目内容
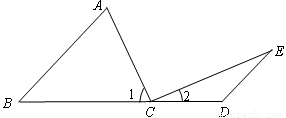
如图:点C在线段BD上,AB∥ED,∠A=∠1,∠E=∠2.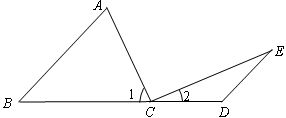
(1)若∠B=40°,求∠1、∠2的度数;
(2)判断AC与CE的位置关系,并说明理由.
(1)∠1=70°,∠2=20°;(2)AC⊥CE
解析试题分析:(1)先根据三角形的内角和定理结合∠A=∠1求得∠1的度数,根据平行线的性质可得∠D的度数,再根据三角形的内角和定理结合∠E=∠2即可求得∠2的度数;
(2)根据三角形的内角和定理结合∠A=∠1可得∠1=90°-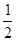 ∠B ,根据平行线的性质可得∠D=180°-∠B,根据三角形的内角和定理结合∠E=∠2可得∠2=
∠B ,根据平行线的性质可得∠D=180°-∠B,根据三角形的内角和定理结合∠E=∠2可得∠2=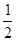 ∠B,即可得到∠ACE的度数.
∠B,即可得到∠ACE的度数.
(1)在⊿ABC中,
∵∠B+∠A+∠1=180°,∠B=40°,∠A=∠1
∴∠1=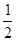 (180°-∠B) =
(180°-∠B) =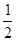 (180°-40 º)=70°
(180°-40 º)=70°
∵AB∥ED
∴∠B+∠D="180°"
∴∠D=180°-40 º =140°
在⊿CDE中,
∵∠D+∠E+∠2=180° ,∠E=∠2,
∴∠2=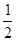 (180°-∠D)=
(180°-∠D)=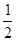 (180°-140 º)=20°;
(180°-140 º)=20°;
(2)AC⊥CE,理由如下:
在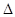 ABC中,
ABC中,
∵∠B+∠A+∠1=180°,∠A=∠1
∴∠1=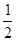 (180°-∠B)=90°-
(180°-∠B)=90°-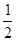 ∠B
∠B
∵AB∥ED
∴∠B+∠D=180°
∴∠D=180°-∠B
在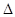 CDE中,
CDE中,
∵∠D+∠E+∠2=180°,∠E=∠2,
∴∠2=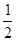 〔180°-∠D〕=
〔180°-∠D〕=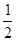 〔180°-(180°-∠B)〕=
〔180°-(180°-∠B)〕=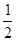 ∠B
∠B
∴∠ACE=180°-(∠1+∠2)=180°-(90°-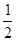 ∠B +
∠B +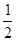 ∠B)=90°
∠B)=90°
∴AC⊥CE.
考点:角的综合题
点评:此类问题知识点多,综合性强,难度较大,熟练掌握三角形中角的关系是解题关键.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
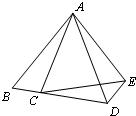 20、如图,点C在线段BD上,△ABD与△ACE都为等边三角形,求∠BDE的度数.
20、如图,点C在线段BD上,△ABD与△ACE都为等边三角形,求∠BDE的度数.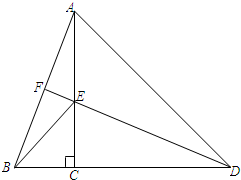 如图,点C在线段BD上,AC⊥BD,CA=CD,点E在线段CA上,且满足DE=AB,连接DE并延长交AB于点F.
如图,点C在线段BD上,AC⊥BD,CA=CD,点E在线段CA上,且满足DE=AB,连接DE并延长交AB于点F.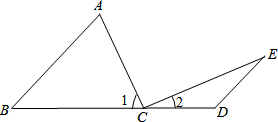 如图:点C在线段BD上,AB∥ED,∠A=∠1,∠E=∠2.
如图:点C在线段BD上,AB∥ED,∠A=∠1,∠E=∠2.