题目内容
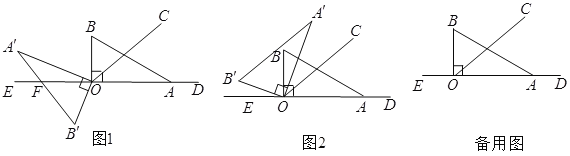
【题目】直线DE上有一点O,过点O在直线DE上方作射线OC,将直角三角板AOB(∠OAB=30°)的直角顶点放在点O处,一条直角边OA在射线OD上,另一边OB在直线DE上方.将直角三角板绕点O按每秒10°的速度逆时针旋转得到三角形A'OB',三角形AOB旋转一周后停止旋转,设旋转时间为t秒.若射线OC的位置保持不变,∠COD=40°.
(1)如图1,在旋转过程中,当边A'B'与直线DE相交于点F时,请用含t的代数式分别表示∠A'OC和∠B'OF的度数,并求出∠A'OC-∠B'OF的值;
(2)如图2,当t=7时,试说明直线A'B'//OC;
(3)在旋转过程中,若t=7,是否还存在某一时刻,使得A'B'//OC;若存在,请求出符合条件的t值;若不存在,请说明理由.
【答案】∠A′OC=10°t-40°,∠B′OF=10°t-90°,50°;(2)详见解析;(3)t=25.
【解析】
(1)根据∠A′OC=∠A′OD-∠COD,∠B′OF=∠B'OB-∠BOF用含t的式子表示出∠A'OC,∠B′OF,然后计算∠A'OC﹣∠B′OF即可;
(2)把t=7代入∠A′OC的表达式,求出∠A′OC的度数,得到∠A′OC=∠A′,根据内错角相等,两直线平行即可得到结论;
(3)根据同旁内角互补,两直线平行,当∠A′OC+∠A′=180°时,A′B′∥OC,列方程得:360°-(10°t-40°)+30°=180°,求解即可.
(1)∠A′OC=∠A′OD-∠COD=10°t-40°,∠B′OF=∠B'OB-∠BOF=10°t-90°,
∠A'OC﹣∠B′OF=(10°t-40°)-(10°t-90°)=50°.
(2)因为t=7,所以∠A′OC=10°×7-40°=30°,
因为∠A′=∠A=30°,
所以∠A′OC=∠A′,
所以A′B′∥OC;(内错角相等,两直线平行)
(3)如图,
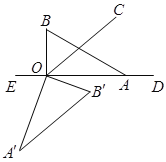
当∠A′OC+∠A′=180°时,
A′B′∥OC,(同旁内角互补,两直线平行)
所以360°-(10°t-40°)+30°=180°,
解得:t=25.

【题目】为积极响应“弘扬传统文化”的号召,某学校倡导全校1200名学生进行经典诗词诵背活动,并在活动之后举办经典诗词大赛,为了解本次系列活动的持续效果,学校团委在活动启动之初,随机抽取部分学生调查“一周诗词诵背数量”,根调查结果绘制成的统计图(部分)如图所示.
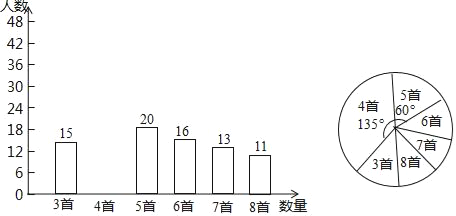
大赛结束后一个月,再次抽查这部分学生“一周诗词诵背数量”,绘制成统计表
一周诗词诵背数量 | 3首 | 4首 | 5首 | 6首 | 7首 | 8首 |
人数 | 10 | 10 | 15 | 40 | 25 | 20 |
请根据调查的信息
(1)活动启动之初学生“一周诗词诵背数量”的中位数为 ;
(2)估计大赛后一个月该校学生一周诗词诵背6首(含6首)以上的人数;
(3)选择适当的统计量,从两个不同的角度分析两次调查的相关数据,评价该校经典诗词诵背系列活动的效果.