题目内容
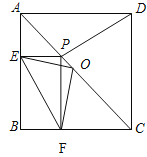
【题目】如图,已知:在正方形ABCD中,点P在AC上,PE⊥AB于E,PF⊥BC于F.
(1)试判断线段EF与PD的长是否相等,并说明理由.
(2)若点O是AC的中点,判断OF与OE之间有怎样的位置和数量关系?并说明理由.
【答案】(1)相等,理由见解析;(2)OF与OE垂直且相等,理由见解析.
【解析】试题分析:(1)连接BP,易证四边形EPFB是矩形,由矩形的性质即可证明EF=PD;
(2)OF与OE垂直且相等,连接BO,证明△EBO与△FCO全等即可.
解:(1)EF=PD,理由如下:
连接BP,
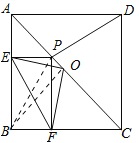
∵四边形ABCD是正方形,
∴∠ABC=90°,AD=AB,∠DAP=∠BAP=45°,
在△BAP和△DAP中,
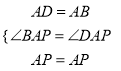 ,
,
∴PD=PB,
∵PE⊥AB于E,PF⊥BC于F,
∴∠PEB=∠PFB=90°,
∴四边形EPFB是矩形,
∴EF=PB,
∴EF=PD;
(2)OF与OE垂直且相等,理由如下:
连接BO,

∵点O是AC的中点,
∴∠EBO=∠FCO=45°,
∵BF=EP,AE=EP,
∴AE=BF,
∴BE=CF,
在△EBO和△FCO中
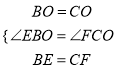 ,
,
∴△EBO≌△FCO,
∴OE=OF,∠EOB=∠COF,
∵OB⊥AC,
∴∠BOC=90°,
∴∠COF+∠BOF=90°,
∴∠EOB+∠BOF=90°,
即OE⊥OF.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

