Question

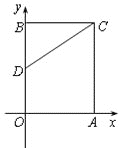
【题目】如图，在平面直角坐标系中，一次函数y=mx+n（m≠0）的图象与反比例函数y= （k≠0）的图象交于第一、三象限内的A、B两点，与y轴交于点C，过点B作BM⊥x轴，垂足为M，BM=OM，OB=2 ，点A的纵坐标为4．
（1）求该反比例函数和一次函数的解析式；
（2）连接MC，求四边形MBOC的面积．

Answer 1

【答案】
（1）解：由题意可得，

BM=OM，OB=2 ，

∴BM=OM=2，

∴点B的坐标为（﹣2，﹣2），

设反比例函数的解析式为y= ，

则﹣2= ，得k=4，

∴反比例函数的解析式为y= ，

∵点A的纵坐标是4，

∴4= ，得x=1，

∴点A的坐标为（1，4），

∵一次函数y=mx+n（m≠0）的图象过点A（1，4）、点B（﹣2，﹣2），

∴ ，得 ，

即一次函数的解析式为y=2x+2；

（2）解：∵y=2x+2与y轴交与点C，

∴点C的坐标为（0，2），

∵点B（﹣2，﹣2），点M（﹣2，0），点O（0，0），

∴OM=2，OC=2，MB=2，

∴四边形MBOC的面积是： = =4．

【解析】（1）根据题意可以求得点B的坐标，从而可以求得反比例函数的解析式，进而求得点A的坐标，从而可以求得一次函数的解析式；（2）根据（1）中的函数解析式可以求得点C，点M、点B、点O的坐标，从而可以求得四边形MBOC的面积．