Question

已知如图所示，在Rt△ABC中，∠C=90°，BC=a，AC=b，AB=c，内切圆O与三边的切点为D、E、F，连接OD、OE．

求证：(1)四边形ODCE为正方形；

(2)设内切圆的半径为r，

求证：．

Answer 1

答案：略
解析：

证明：(1)∵OD⊥AC，OE⊥BC，∠C=90°，∴四边形ODCE为矩形． ∵CD=CE，∴四边形ODCE为正方形． (2)由切线长定理可知 AF=AD=b－r，BF=BE=a－r， ∵AF＋BF=c，∴b－r＋a－r=c． 即．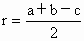

提示：

(1)有一组邻边相等的矩形为正方形． (2)应用切线长定理得出公式，在以后的学习中经常用到．