题目内容
如图①，将一张直角三角形纸片ABC折叠，使点A与点C重合，这时DE为折痕，△CBE为等腰三角形，再继续将纸片沿△CBE的对称轴EF折叠，这时得到了两个完全重合的矩形（其中一个是原三角形的内接矩形，另一个是拼合成的无缝隙、无重叠的矩形），我们称这样的两个矩形为“叠加矩形”．请完成下列问题：
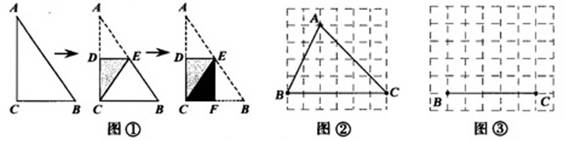
1.如图②，正方形网格中的△ABC能折叠成“叠加矩形”吗？如能，请在图②中画出折痕；
2.如图③，在正方形网格中，以给定的BC为一边，画出一个斜△ABC，使其顶点A在格点上，且△ABC折成的“叠加矩形”为正方形；
3.如果一个三角形所折成的“叠加矩形” 为正方形，那么它必须满足的条件是 ．
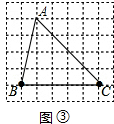
1.如图②所示：
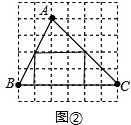
2.如图③所示：
3.由（2）可得，若一个三角形所折成的“叠加矩形”为正方形，
那么三角形的一边长与该边上的高相等的直角三角形或锐角三角形．
解析:
1.应先在三角形的格点中找一个矩形，折叠即可；
2.根据正方形的边长应等于底边及底边上高的一半可得所求三角形的底边与高相等；
3.由（2）可得相应结论
练习册系列答案
相关题目
