题目内容
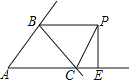
【题目】在△ABC中,∠ABC和∠ACB的外角平分线BP,CP交于点P,PE⊥AC于点E,若S△BPC=3、PE=2,S△ABC=5,求△ABC的周长是______.
【答案】11
【解析】
过点P作PD⊥AB于点D、PF⊥BC于点F,根据角平分线上的点到角的两边距离相等可得PF= PE,再根据三角形的面积求出BC,然后求出AC+AB,再根据S△ABC=S△ACP+S△ABP-S△BCP计算即可得解.
过点P分别作PD⊥AB于点D、PF⊥BC于点F,连接AP,如图:
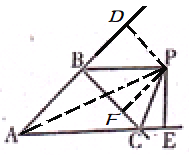
在△ABC中,∠ABC和∠ACB的外角平分线BP、CP交于点P,PE⊥AC于点E,PE=2,
∴PF=PE=2,PD=PF=2,
因为S△BPC=3,S△ABC=5,
![]() ,
,
S△PAB+ S△PAC =S△ABC +S△BPC =8即
![]() ,
,
∴BC=3,AB+AC=8,
∴AB+BC+AC=3+8=11,
即△ABC的周长是11,
故答案为:11.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
【题目】某出租车驾驶员从公司出发,在南北向的人民路上连续接送5批客人.行驶路程记录如下(规定向南为正,向北为负,单位:![]() ):
):
第1批 | 第2批 | 第3批 | 第4批 | 第5批 |
5 | 2 | -4 | -3 | 10 |
(1)接送完第5批客人后,该驾驶员在公司 边(填南或北),距离公司 千米.
(2)若该出租车每千米耗油0.2升,那么在这过程中共耗油 升.
(3)若该出租车的计价标准为:行驶路程不超过3![]() 收费10元,超过3
收费10元,超过3![]() 的部分按每千米1.8元收费,在这过程中该驾驶员共收到车费多少元?
的部分按每千米1.8元收费,在这过程中该驾驶员共收到车费多少元?