Question

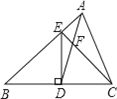
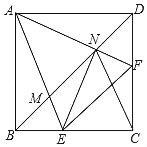
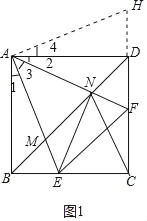
【题目】如图，在正方形ABCD中，点E、F分别在边BC、DC上，AE、AF分别交BD于点M、N，连接CN、EN，且CN＝EN．下列结论：①AN＝EN，AN⊥EN；②BE+DF＝EF；③；④图中只有4对相似三角形，其中正确结论的个数是（　　）

A. 4B. 3C. 2D. 1

Answer 1

【答案】B

【解析】

①证明△NBA≌△NBC，∠ABE+∠ANE＝180°即可解决问题；

②证明△AFH≌△AFE即可；

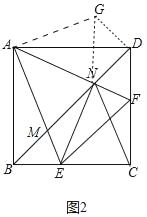
③如图2中，首先证明△AMN∽△AFE，可得，即可解决问题；

④相似三角形不止4对相似三角形．

将△ABE绕点A逆时针旋转90°得到△ADH．

∵四边形ABCD是中正方形，

∴AB＝BC＝AD，∠BAD＝∠ABC＝90°，∠ABD＝∠CBD＝45°，

在△BNA和△BNC中，

，

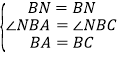∴△NBA≌△NBC（SAS），

∴AN＝CN，∠BAN＝∠BCN，

∵EN＝CN，

∴AN＝EN，∠NEC＝∠NCE＝∠BAN，

∵∠NEC+∠BEN＝180°，

∴∠BAN+∠BEN＝180°，

∴∠ABC+∠ANE＝180°，

∴∠ANE＝90°，

∴AN＝NE，AN⊥NE，故①正确，

∴∠3＝∠AEN＝45°，

∵∠3＝45°，∠1＝∠4，

∴∠2+∠4＝∠2+∠1＝45°，

∴∠3＝∠FAH＝45°，∵AF＝AF，AE＝AH，

∴△AFE≌△AFH（SAS），

∴EF＝FH＝DF+DH＝DF+BE，∠AFH＝∠AFE，故②正确，

∵∠MAN＝∠EAF，∠AMN＝∠AFE，

∴△AMN∽△AFE，

∴，

故③正确，

图中相似三角形有△ANE∽△BAD～△BCD，△ANM∽△AEF，△ABN∽△FDN，△BEM∽△DAM等，故④错误，

故选B．