题目内容
如图,直线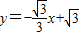 与x轴、y轴分别交于点A、B,已知点P是第一象限内的点,由点P、O、B组成了一个含60°的直角三角形,则点P的坐标
与x轴、y轴分别交于点A、B,已知点P是第一象限内的点,由点P、O、B组成了一个含60°的直角三角形,则点P的坐标为 .

【答案】分析:先根据一次函数方程式求出A、B两点的坐标,然后根据已知条件,进行分类讨论分别求出点P的坐标.
解答:解:直线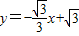 与x轴、y轴分别交于点A、B,
与x轴、y轴分别交于点A、B,
当y=0时,x=3,当x=0时,y=-4;
故A、B两点坐标分别为A(3,0),B(0,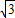 ),
),
∵点P是第一象限内的点且点P、O、B组成了一个含60°的直角三角形,
①当∠PBO=90°,∠POB=60°时,P点坐标为P(3,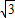 );
);
②当∠OPB=90°,∠POB=60°时,P点坐标为P( ,
,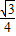 );
);
③当∠PBO=90°,∠OPB=60°时,P点坐标为P(1,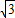 );
);
④当∠PBO=90°,∠POB=60°时,P点坐标为P( ,
,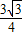 ).
).
故答案为:P1(3,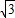 ),P2(1,
),P2(1,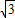 ),P3(
),P3( ,
,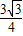 ),P4(
),P4(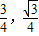 ).
).
点评:本题主要考查了一次函数的应用,做题时要注意数形结合思想和分类讨论思想的运用,是各地的中考热点,学生在平常要多加训练,属于中档题.
解答:解:直线
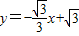 与x轴、y轴分别交于点A、B,
与x轴、y轴分别交于点A、B,当y=0时,x=3,当x=0时,y=-4;
故A、B两点坐标分别为A(3,0),B(0,
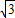 ),
),∵点P是第一象限内的点且点P、O、B组成了一个含60°的直角三角形,
①当∠PBO=90°,∠POB=60°时,P点坐标为P(3,
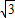 );
);②当∠OPB=90°,∠POB=60°时,P点坐标为P(
 ,
,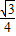 );
);③当∠PBO=90°,∠OPB=60°时,P点坐标为P(1,
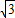 );
);④当∠PBO=90°,∠POB=60°时,P点坐标为P(
 ,
,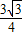 ).
).故答案为:P1(3,
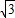 ),P2(1,
),P2(1,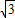 ),P3(
),P3( ,
,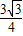 ),P4(
),P4(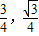 ).
).点评:本题主要考查了一次函数的应用,做题时要注意数形结合思想和分类讨论思想的运用,是各地的中考热点,学生在平常要多加训练,属于中档题.

练习册系列答案
相关题目
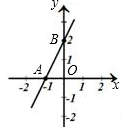 如图,直线与x轴、y轴分别交于A、B两点.
如图,直线与x轴、y轴分别交于A、B两点.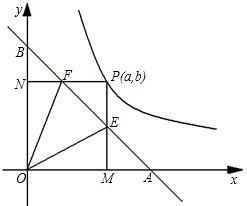
 3、如图,直线与y轴的交点是(0,-3),则当x<0时,( )
3、如图,直线与y轴的交点是(0,-3),则当x<0时,( ) 如图,直线与x轴、y轴分别交于A、B两点.
如图,直线与x轴、y轴分别交于A、B两点. 与x轴、y轴分别交于B、C两点,点A在x轴负半轴上,且
与x轴、y轴分别交于B、C两点,点A在x轴负半轴上,且 ,抛物线经过A、B、C三点,D为线段AB中点,点P(m,n)是该抛物线上的一个动点(其中m>0,n<0),连接DP交BC于点E.
,抛物线经过A、B、C三点,D为线段AB中点,点P(m,n)是该抛物线上的一个动点(其中m>0,n<0),连接DP交BC于点E.