题目内容
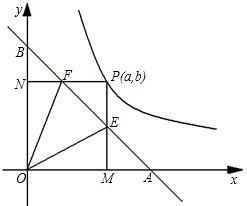
如图,直线与x轴、y轴交于A、B两点,且OA=OB=1,点P是反比例函数y=| 1 |
| 2x |
(1)设交点E、F都在线段AB上,分别求出点E、点F的坐标;(用含a的代数式表示)
(2)△AOF与△BOE是否一定相似?如果一定相似,请予以证明;如果不一定相似或一定不相似,请简短说明理由;
(3)当点P在曲线上移动时,△OEF随之变动,指出在△OEF的三个内角中,大小始终保持不变的那个角和它的大小,并证明你的结论;
(4)在双曲线y=
| 1 |
| 2x |
分析:(1)设直线EF的解析式为y=kx+b,把A(1,0),B(0,1)代入y=kx+b,运用待定系数法求出直线EF的解析式,由点P(a,b)是反比例函数y=
图象上的点,得出b=
,又点E的横坐标为a,点F的纵坐标为b即
,分别把x=a,y=
代入直线EF的解析式,即可求出对应的值,从而得出结果;
(2)在△BOE与△AOF中,由于∠OBA=∠OAB=45°,根据相似三角形的判定,可分别计算BE:OB与OA:AF的值,如果它们相等,那么△AOF∽△BEO,否则,就不相似;
(3)根据相似三角形的对应角相等及三角形的一个外角等于与它不相邻的两个外角的和得出∠FOE=∠EAO=45°;
(4)假设在双曲线y=
上存在点P,使点P到直线AB的距离最短.那么平行于AB的直线y=-x+m应与双曲线y=
相切,即方程-x+m=
有两个相等的实数根,根据判别式△=0求出m的值,从而确定点P的坐标,进而得到点P到直线AB的最短距离.
| 1 |
| 2x |
| 1 |
| 2a |
| 1 |
| 2a |
| 1 |
| 2a |
(2)在△BOE与△AOF中,由于∠OBA=∠OAB=45°,根据相似三角形的判定,可分别计算BE:OB与OA:AF的值,如果它们相等,那么△AOF∽△BEO,否则,就不相似;
(3)根据相似三角形的对应角相等及三角形的一个外角等于与它不相邻的两个外角的和得出∠FOE=∠EAO=45°;
(4)假设在双曲线y=
| 1 |
| 2x |
| 1 |
| 2x |
| 1 |
| 2x |
解答:解:(1)设直线EF的解析式为y=kx+b,
由题知A(1,0),B(0,1),
把A(1,0),B(0,1)代入y=kx+b,
得k+b=0,b=1,
解得k=-1,b=1.
∴y=-x+1.
∵点P(a,b)是反比例函数y=
图象上的点,
∴b=
.
∴E(a,1-a),F(1-
,
);
(2)△AOF与△BOE一定相似.
理由如下:
∵OA=OB=1,
∴AB=
,∠OBA=∠OAB=45°,
∴AE=
AM=
(1-a),BF=
BN=
(1-
),
∴BE=BA-AE=
a,AF=BA-BF=
,
∴BE•AF=
•
a=1=OA•OB=1,
∴
=
,
又∵∠OBA=∠OAB=45°,
∴△AOF∽△BEO;
(3)∠FOE=45°,角度始终不变.
理由如下:
∵△AOF∽△BEO,
∴∠FOA=∠OEB,
∴∠FOE+∠EOA=∠EOA+∠EAO,
得∠FOE=∠EAO=45°;
(4)设平行于直线AB的直线解析式为y=-x+m,
解方程-x+m=
,
化简得2x2-2mx+1=0,
当△=0时,解得m=±
(负值舍去).
所以2x2-2
x+1=0,解得x=
.
所以点P的坐标为(
,
).
∴点P到直线AB的距离最短为(
-1)×sin45°=1-
.
由题知A(1,0),B(0,1),
把A(1,0),B(0,1)代入y=kx+b,
得k+b=0,b=1,
解得k=-1,b=1.
∴y=-x+1.
∵点P(a,b)是反比例函数y=
| 1 |
| 2x |
∴b=
| 1 |
| 2a |
∴E(a,1-a),F(1-
| 1 |
| 2a |
| 1 |
| 2a |
(2)△AOF与△BOE一定相似.
理由如下:
∵OA=OB=1,
∴AB=
| 2 |
∴AE=
| 2 |
| 2 |
| 2 |
| 2 |
| 1 |
| 2a |
∴BE=BA-AE=
| 2 |
| ||
| 2a |
∴BE•AF=
| ||
| 2a |
| 2 |
∴
| BE |
| OB |
| OA |
| AF |
又∵∠OBA=∠OAB=45°,
∴△AOF∽△BEO;
(3)∠FOE=45°,角度始终不变.
理由如下:
∵△AOF∽△BEO,
∴∠FOA=∠OEB,
∴∠FOE+∠EOA=∠EOA+∠EAO,
得∠FOE=∠EAO=45°;
(4)设平行于直线AB的直线解析式为y=-x+m,
解方程-x+m=
| 1 |
| 2x |
化简得2x2-2mx+1=0,
当△=0时,解得m=±
| 2 |
所以2x2-2
| 2 |
| ||
| 2 |
所以点P的坐标为(
| ||
| 2 |
| ||
| 2 |
∴点P到直线AB的距离最短为(
| 2 |
| ||
| 2 |
点评:本题主要考查了运用待定系数法求函数的解析式,相似三角形的判定及性质,一次函数与反比例函数的关系,通过解方程求交点坐标等知识.综合性强,有一定难度.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
 如图,直线与x轴、y轴分别交于A、B两点.
如图,直线与x轴、y轴分别交于A、B两点. 3、如图,直线与y轴的交点是(0,-3),则当x<0时,( )
3、如图,直线与y轴的交点是(0,-3),则当x<0时,( ) 如图,直线与x轴、y轴分别交于A、B两点.
如图,直线与x轴、y轴分别交于A、B两点. 与x轴、y轴分别交于B、C两点,点A在x轴负半轴上,且
与x轴、y轴分别交于B、C两点,点A在x轴负半轴上,且 ,抛物线经过A、B、C三点,D为线段AB中点,点P(m,n)是该抛物线上的一个动点(其中m>0,n<0),连接DP交BC于点E.
,抛物线经过A、B、C三点,D为线段AB中点,点P(m,n)是该抛物线上的一个动点(其中m>0,n<0),连接DP交BC于点E.