题目内容
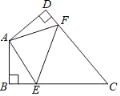
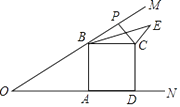
【题目】如图,在Rt△ABC中,∠C=90°,BD平分∠ABC,交AC于D,DE⊥AB于E,EF∥BC交AC于F.
(1)求证:△EDF∽△ADE;
(2)猜想:线段DC,DF、DA之间存在什么关系?并说明理由.
【答案】
(1)证明:∵DE⊥AB,
∴∠AED=90°,
∵EF∥BC,
∴∠AFE=∠C=90°,
∴∠DFE=∠DEA,
而∠FDE=∠EDA,
∴△EDF∽△ADE;
(2)解:DC2=DFDA.理由如下:
∵△EDF∽△ADE,
∴DE:DA=DF:DE,
即DE2=DFDA,
∵BD平分∠ABC,DE⊥AB,DC⊥BC,
∴DE=DC,
∴DC2=DFDA
【解析】(1)两三角形已有直角对应相等,只需再证一个角相等即可,利用余角性质即可;(2)由相似三角形的判定可得出比例式,变形为乘积式.
【考点精析】认真审题,首先需要了解相似三角形的判定与性质(相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方).

练习册系列答案
相关题目