题目内容
【题目】已知:在![]() 中,
中,![]() .
.
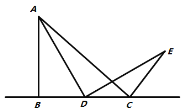
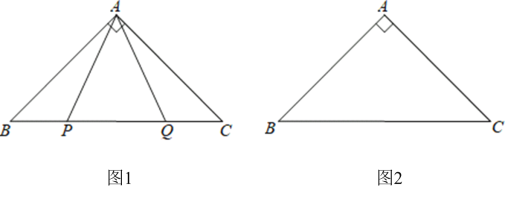
(1)如图1,![]() 是
是![]() 边上两点,
边上两点,![]() , 求
, 求![]() 的度数.
的度数.
(2)点![]() 是
是![]() 边上两动点(不与
边上两动点(不与![]() 重合), 点
重合), 点![]() 在点
在点![]() 左侧,且
左侧,且![]() ,点
,点![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() ,连接
,连接![]() .
.
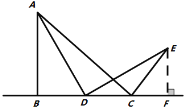
①依题意将图2补全.
②小明通过观察和实验,提出猜想:在点![]() 运动的过程中,始终有
运动的过程中,始终有![]() 为等腰直角三角形,他把这个猜想与同学们进行交流,通过讨论,形成以下证明猜想的思路:要想证明
为等腰直角三角形,他把这个猜想与同学们进行交流,通过讨论,形成以下证明猜想的思路:要想证明![]() 为等腰直角三角形,只需证
为等腰直角三角形,只需证![]() .
.
请参考上面的思路,帮助小明证明△APM 为等腰直角三角形.
【答案】(1)![]() ;(2)①图见解析,②证明见解析
;(2)①图见解析,②证明见解析
【解析】
(1)首先证明∠BAP=∠CAQ,再根据三角形的外角的性质计算即可;
(2)①根据要求画出图形即可;
②只要证明AP=AM,∠PAM=90°即可证明△APM 为等腰直角三角形;
解:(1)∵![]() 为等腰直角三角形,
为等腰直角三角形,
∴![]()
∴![]()
∵![]() .
.
∴![]() ;
;
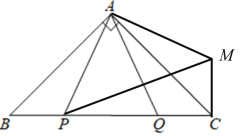
(2)①补全图形,如图所示,

②证明:如图,连接![]() .
.
∵![]() 为等腰直角三角形,
为等腰直角三角形,
∴![]()
又∵![]() ,
,
∴![]() .
.
∴![]() .
.
∴△APB≌△AQC(AAS)
∴![]() ,
,
又![]() .
.
![]()
又∵![]() ,
,
∴![]()
∴![]() 为等腰直角三角形.
为等腰直角三角形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】为了解某市区九年级学生每天的健身活动情况,随机从市区九年级的12000名学生中抽取了500名学生,对这些学生每天的健身活动时间进行统计整理,作出了如下不完整的统计图(每组数据含最小值不含最大值,统计数据全部为整数),请根据以下信息解答如下问题:
时间/分 | 频数 | 频率 |
30~40 | 25 | 0.05 |
40~50 | 50 | 0.10 |
50~60 | 75 | b |
60~70 | a | 0.40 |
70~80 | 150 | 0.30 |
(1)a=_______,b=_______;
(2)请补全频数分布直方图;
(3)学生每天健身时间的中位数会落在哪个时间段?
(4)若每天健身时间在60分钟以上为符合每天“阳光一小时”的规定,则符合规定的学生人数大约是多少人?