题目内容
如图,抛物线 交坐标轴于A、B、D三点,过点D作
交坐标轴于A、B、D三点,过点D作 轴的平行线交抛物线于点C.直线l过点E(0,-
轴的平行线交抛物线于点C.直线l过点E(0,- ),且平分梯形ABCD面积.
),且平分梯形ABCD面积.
⑴ 直接写出A、B、D三点的坐标;
⑵ 直接写出直线l的解析式;
⑶ 若点P在直线l上,且在x轴上方,tan∠OPB= ,求点P的坐标.
,求点P的坐标.

 交坐标轴于A、B、D三点,过点D作
交坐标轴于A、B、D三点,过点D作 轴的平行线交抛物线于点C.直线l过点E(0,-
轴的平行线交抛物线于点C.直线l过点E(0,- ),且平分梯形ABCD面积.
),且平分梯形ABCD面积.⑴ 直接写出A、B、D三点的坐标;
⑵ 直接写出直线l的解析式;
⑶ 若点P在直线l上,且在x轴上方,tan∠OPB=
 ,求点P的坐标.
,求点P的坐标.
⑴点A(-2,0),点B(8,0),点D(0,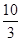 );⑵ 直线l:
);⑵ 直线l: ;⑶(7,7).
;⑶(7,7).
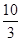 );⑵ 直线l:
);⑵ 直线l: ;⑶(7,7).
;⑶(7,7).试题分析:⑴令
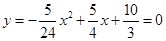 ,解之即可求得A,B的坐标;在
,解之即可求得A,B的坐标;在 中,令
中,令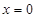 ,解之即可求得D的坐标.
,解之即可求得D的坐标.⑵作CF⊥x轴,F为垂足.先求出矩形OFCD的中心坐标M(3,
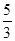 ),则直线ME即为所求直线l.[
),则直线ME即为所求直线l.[⑶若点P为所求的点,画出△POB的外接圆⊙G,并作GH⊥x轴,H为垂足,则∠OGH=∠HGB=∠OPB;
作PN⊥x轴,GN∥x轴,交于点N,则GN=3,PN=4,因此点P的坐标为(7,7).
⑴ 点A(-2,0),点B(8,0),点D(0,
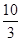 ).
).⑵ 直线l:
 .
.⑶ 如图,若点P为所求的点,画出△POB的外接圆⊙G,并作GH⊥x轴,H为垂足,则∠OGH=∠HGB=∠OPB.
∵OH=HB=4,tan∠OGH=tan∠HGB=tan∠OPB=
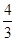 ,
,∴GH=3,GO=GB=GP=5,即⊙G的圆心G坐标为(4,3),半径r=5.
将点G坐标代入直线l解析式发现,点G恰巧在直线l上.
设直线l与x轴交于点Q,不难计算GH:QH=4:3.
作PN⊥x轴,GN∥x轴,交于点N,则GN=3,PN=4,
因此点P的坐标为(7,7).
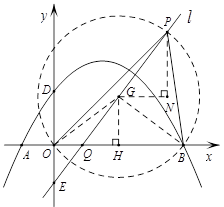

练习册系列答案
相关题目
 (x>0)图象上一个动点,以P为圆心的圆始终与y轴相切,设切点为A.
(x>0)图象上一个动点,以P为圆心的圆始终与y轴相切,设切点为A. ?若存在,试求出所有满足条件的M点的坐标;若不存在,试说明理由.
?若存在,试求出所有满足条件的M点的坐标;若不存在,试说明理由.
 x2+mx+n的图象经过A,C两点.
x2+mx+n的图象经过A,C两点.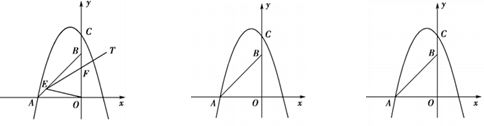
 )倍.若存在,请直接写出点P坐标;若不存在,请说明理由.
)倍.若存在,请直接写出点P坐标;若不存在,请说明理由.
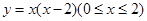 的图象,记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3;……如此进行下去,直至得C14. 若P(27,m)在第14段图象C14上,则m= .
的图象,记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3;……如此进行下去,直至得C14. 若P(27,m)在第14段图象C14上,则m= .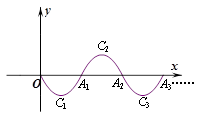
 的最小值为负数,则m的取值范围是( )
的最小值为负数,则m的取值范围是( )