题目内容
如图,两个标有数字的轮子可以分别绕轮子的中心旋转,旋转停止时,每个轮子上方的箭头各指着轮子上的一个数字,若左图轮子上方的箭头指着的数字为a,右图轮子上方的箭头指的数字为b,数对(a,b)所有可能的个数为n,其中a+b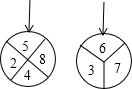 恰为偶数的不同个数为m,则
恰为偶数的不同个数为m,则
等于( )
 恰为偶数的不同个数为m,则
恰为偶数的不同个数为m,则| m |
| n |
A、
| ||
B、
| ||
C、
| ||
D、
|
分析:先用树状图展示所有可能的结果,共有12种等可能结果数,然后找出和为偶数的个数,这样即可得到
的值.
| m |
| n |
解答:解:列树状图:
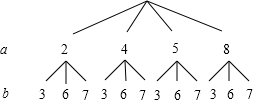
∴数对(a,b)所有可能的个数为n=12,
其中a+b恰为偶数的不同个数为m=5,
∴
=
,
故选C.

∴数对(a,b)所有可能的个数为n=12,
其中a+b恰为偶数的不同个数为m=5,
∴
| m |
| n |
| 5 |
| 12 |
故选C.
点评:本题考查了利用树状图展示所有等可能的结果的方法.

练习册系列答案
相关题目
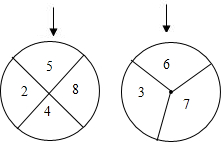 如图,两个标有数字的轮子可以分别绕轮子中心旋转,旋转停止时,每个轮子上方的箭头各指着轮子上的一个数字,这两个数字和为偶数的概率是( )
如图,两个标有数字的轮子可以分别绕轮子中心旋转,旋转停止时,每个轮子上方的箭头各指着轮子上的一个数字,这两个数字和为偶数的概率是( )A、
| ||
B、
| ||
C、
| ||
D、
|
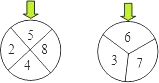 如图,两个标有数字的轮子可以分别绕轮子的中心旋转,旋转停止时,每个轮子上方的箭头各指着轮子上的一个数字,若左图轮子上方的箭头指着的数字为a,右图轮子上方的箭头指着的数字为b,数对(a,b)所有可能的个数为n,其中a+b恰为偶数的不同数对的参数为m,则m/n等于( )
如图,两个标有数字的轮子可以分别绕轮子的中心旋转,旋转停止时,每个轮子上方的箭头各指着轮子上的一个数字,若左图轮子上方的箭头指着的数字为a,右图轮子上方的箭头指着的数字为b,数对(a,b)所有可能的个数为n,其中a+b恰为偶数的不同数对的参数为m,则m/n等于( )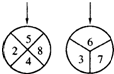 如图,两个标有数字的轮子可以分别绕轮子的中心旋转,旋转停止时,每个轮子上方的箭头各指着轮子上的一个数字,若左图轮子上方的箭头指着的数字为a,右图轮子上方的箭头指着的数字为b,数对(a,b)所有可能的个数为n,其中a+b恰为偶数的不同数对的参数为m,则
如图,两个标有数字的轮子可以分别绕轮子的中心旋转,旋转停止时,每个轮子上方的箭头各指着轮子上的一个数字,若左图轮子上方的箭头指着的数字为a,右图轮子上方的箭头指着的数字为b,数对(a,b)所有可能的个数为n,其中a+b恰为偶数的不同数对的参数为m,则 如图,两个标有数字的轮子可以分别绕轮子中心旋转,旋转停止时,每个轮子上方的箭头各指着轮子上的一个数字,这两个数字和为偶数的概率是( )
如图,两个标有数字的轮子可以分别绕轮子中心旋转,旋转停止时,每个轮子上方的箭头各指着轮子上的一个数字,这两个数字和为偶数的概率是( ) 如图,两个标有数字的轮子分别被等分为4部分和3部分,它们可以分别绕轮子中心旋转,旋转停止时,每个轮子上方的箭头各指着轮子上的一个数字,这两个数字的和为偶数的概率是( )
如图,两个标有数字的轮子分别被等分为4部分和3部分,它们可以分别绕轮子中心旋转,旋转停止时,每个轮子上方的箭头各指着轮子上的一个数字,这两个数字的和为偶数的概率是( )