题目内容
 23、如图,已知AC=CE,∠1=∠2=∠3.
23、如图,已知AC=CE,∠1=∠2=∠3.(1)说明∠B=∠D的理由;
(2)说明AB=DE的理由.
分析:(1)根据∠1=∠2可得出∠B=∠D,再由∠2=∠3,可得出∠ACB=∠ECD,从而证明△ABC≌△EDC,则∠B=∠D;
(2)由△ABC≌△EDC,则AB=DE.
(2)由△ABC≌△EDC,则AB=DE.
解答:解:(1)∵∠1=∠2,
∴∠B=∠D,
∴∠2=∠3,∴∠2+∠ACD=∠3+∠ACD,
即∠ACB=∠ECD,
∴△ABC≌△EDC,
∴∠B=∠D;
(2)∵△ABC≌△EDC(已证),
∴AB=DE(全等三角形的对应边相等).
∴∠B=∠D,
∴∠2=∠3,∴∠2+∠ACD=∠3+∠ACD,
即∠ACB=∠ECD,
∴△ABC≌△EDC,
∴∠B=∠D;
(2)∵△ABC≌△EDC(已证),
∴AB=DE(全等三角形的对应边相等).
点评:本题考查了全等三角形的判定和性质以及等式的基本性质,是基础知识要熟练掌握.

练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
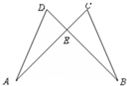 19、如图,已知AC与BD相交于点E,DE=CE,AE=BE.求证:∠A=∠B.
19、如图,已知AC与BD相交于点E,DE=CE,AE=BE.求证:∠A=∠B.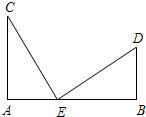 28、如图,已知AC⊥AB,DB⊥AB,AC=BE,AE=BD,试猜想线段CE与DE的大小与位置关系,并证明你的结论.
28、如图,已知AC⊥AB,DB⊥AB,AC=BE,AE=BD,试猜想线段CE与DE的大小与位置关系,并证明你的结论.
