题目内容
方程ax2+2x+1=0至少有一个负根,则a的取值范围是________.
a≤1.
分析:方程ax2+2x+1=0为一个类二次方程,故我们要分a=0和a≠0两种情况进行讨论,当a=0时方程为一次方程,可直接求解进行判断,当a≠0时,方程为二次方程,可利用韦达定理进行判断.
解答:当a=0时,方程可化为2x+1=0
此时方程有一个根,满足条件,
当a≠0时,方程ax2+2x+1=0时为二次方程,若方程有根
则△=4-4a≥0,解得a≤1,a≠0
若方程无负根,由韦达定理得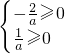 ,
,
不存在满足条件的a值,
即当a≤1,a≠0时,方程至少有一个负根
综上所述满足条件的a的取值范围是a≤1
故答案为a≤1.
点评:本题考查的知识点是一元二次方程的根的分面与系数的关系,其中本题易忽略对a=0的讨论,另外熟练掌握是韦达定理是解答本题的关键.
分析:方程ax2+2x+1=0为一个类二次方程,故我们要分a=0和a≠0两种情况进行讨论,当a=0时方程为一次方程,可直接求解进行判断,当a≠0时,方程为二次方程,可利用韦达定理进行判断.
解答:当a=0时,方程可化为2x+1=0
此时方程有一个根,满足条件,
当a≠0时,方程ax2+2x+1=0时为二次方程,若方程有根
则△=4-4a≥0,解得a≤1,a≠0
若方程无负根,由韦达定理得
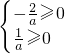 ,
,不存在满足条件的a值,
即当a≤1,a≠0时,方程至少有一个负根
综上所述满足条件的a的取值范围是a≤1
故答案为a≤1.
点评:本题考查的知识点是一元二次方程的根的分面与系数的关系,其中本题易忽略对a=0的讨论,另外熟练掌握是韦达定理是解答本题的关键.

练习册系列答案
相关题目
已知反比例函数y=
,当x>0时,y随x的增大而增大,则关于x的方程ax2-2x+b=0的根的情况是( )
| ab |
| x |
| A、有两个正根 |
| B、有两个负根 |
| C、有一个正根一个负根 |
| D、没有实数根 |