题目内容
(2006•惠安县质检)如图,等腰直角三角形ABC的斜边BC在x轴上,且BC=4,点D是BC的中点,点A在第一象限内,AB与y轴相交于点E.已知点B(-1,0),点P是AC上的一个动点(与点A、C不重合).(1)请直接写出A、E的坐标;
(2)若抛物线y=-
 x2+bx+c过点A、E,求抛物线的解析式;
x2+bx+c过点A、E,求抛物线的解析式;(3)连接PB、PD,设△PBD的周长为L,请通过画图(不必写画法)找出点P在什么位置时,L取最小值,求点P的坐标,并判断此时点P是否在(2)中的抛物线上,请说明理由.
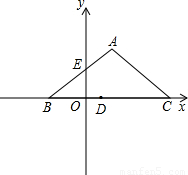
【答案】分析:(1)由于三角形ABC是等腰直角三角形,而D是BC的中点,如果连接AD,那么AD就垂直平分BC,根据BC=4和B点的坐标即可得出BD=AD=CD=2,那么D的坐标是(1,0),C(3,0),A(1,2).而∠ABC=45°,因此直角三角形BOE中,BO=OE=1,因此E的坐标是(0,1).
(2)根据(1)的A,E的坐标,可用待定系数法求函数的解析式.
(3)当L最小时,点P应该是D关于AC对称的点与B点的连线,两线相交的交点就是P点.那么求P的坐标就要求出直线BD′和直线AC的解析式.根据D关于AC对称,可求出D′的坐标,那么有了B,D′,A,C四点的坐标,可用待定系数法求出两条直线的解析式,然后将两个函数式联立方程组即可求出P的坐标.然后将P的坐标代入(2)的函数式中,从而判断出P点是否在抛物线上.
解答: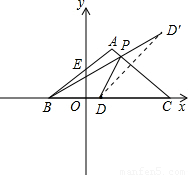 解:(1)A(1,2),E(0,1);
解:(1)A(1,2),E(0,1);
(2)依题意得: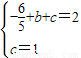
解得: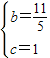
∴y=- x2+
x2+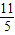 x+1;
x+1;
(3)通过画图找出点P的位置,如图所示.
设点D(1,0)关于直线AC的对称点D′
由对称性可求D′(3,2)
直线AC过A(1,2),C(3,0)
设y=k1x+b1,则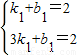
解得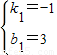 ∴y=-x+3
∴y=-x+3
直线BD′过点B(-1,0),D′(3,2)
设y=k2x+b2,则 ,
,
解得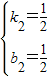 ∴y=
∴y= x+
x+
由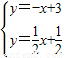
解得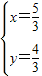
∴交点坐标为( ,
, )
)
当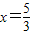 x=
x= 时,y=-
时,y=- ×(
×( )2+
)2+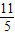 ×
× +1=
+1=
∴点P在抛物线上.
点评:本题主要考查了用待定系数法求一次函数及二次函数的解析式,(3)中正确地作出P点的位置是解题的关键.
(2)根据(1)的A,E的坐标,可用待定系数法求函数的解析式.
(3)当L最小时,点P应该是D关于AC对称的点与B点的连线,两线相交的交点就是P点.那么求P的坐标就要求出直线BD′和直线AC的解析式.根据D关于AC对称,可求出D′的坐标,那么有了B,D′,A,C四点的坐标,可用待定系数法求出两条直线的解析式,然后将两个函数式联立方程组即可求出P的坐标.然后将P的坐标代入(2)的函数式中,从而判断出P点是否在抛物线上.
解答:
 解:(1)A(1,2),E(0,1);
解:(1)A(1,2),E(0,1);(2)依题意得:
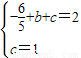
解得:
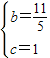
∴y=-
 x2+
x2+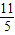 x+1;
x+1;(3)通过画图找出点P的位置,如图所示.
设点D(1,0)关于直线AC的对称点D′
由对称性可求D′(3,2)
直线AC过A(1,2),C(3,0)
设y=k1x+b1,则
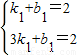
解得
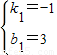 ∴y=-x+3
∴y=-x+3直线BD′过点B(-1,0),D′(3,2)
设y=k2x+b2,则
 ,
,解得
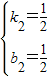 ∴y=
∴y= x+
x+
由
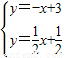
解得
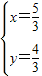
∴交点坐标为(
 ,
, )
)当
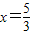 x=
x= 时,y=-
时,y=- ×(
×( )2+
)2+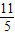 ×
× +1=
+1=
∴点P在抛物线上.
点评:本题主要考查了用待定系数法求一次函数及二次函数的解析式,(3)中正确地作出P点的位置是解题的关键.

练习册系列答案
相关题目