题目内容
（2006•惠安县质检）已知，如图，∠AOB=30°，M为OB边上任意一点，以M为圆心，r为半径的⊙M，当⊙M与OA相切时，OM=2cm，则r= cm．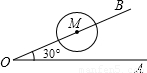
【答案】分析：根据直角三角形内，30°的角所对的直角边是斜边的一半可求得r的值．
解答：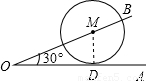
解：当⊙M与OA相切时，MB=r，∠MDO=90°；
∵∠AOB=30°，OM=2cm，
∴r=
OM=1cm．
点评：当圆与直线相切时，根据切线的性质定理，切线垂直于半径，可构成直角三角形，从而解决问题．
解答：
解：当⊙M与OA相切时，MB=r，∠MDO=90°；∵∠AOB=30°，OM=2cm，
∴r=
OM=1cm．点评：当圆与直线相切时，根据切线的性质定理，切线垂直于半径，可构成直角三角形，从而解决问题．
练习册系列答案
快捷英语周周练系列答案
相关题目
x2+bx+c过点A、E，求抛物线的解析式；
