题目内容
如图,AD⊥BC于D,EG⊥BC于G,∠E=∠1,求证:AD平分∠BAC。
根据垂直的定义可得∠ADC=∠EGC=90°,即可证得AD∥EG,根据平行线的性质可得∠1=∠2,∠E=∠3,再结合∠E=∠1可得∠2=∠3,从而可以证得结论.
解析试题分析:证明:∵AD⊥BC,EG⊥BC
∴∠ADC=∠EGC=90°
∴AD∥EG
∴∠1=∠2,∠E=∠3
∵∠E=∠1
∴∠2=∠3
∴AD平分∠BAC.
考点:平行线的判定和性质
点评:平行线的判定和性质是初中数学的重点,贯穿于整个初中数学的学习,是中考中比较常见的知识点,一般难度不大,需熟练掌握.

练习册系列答案
相关题目
已知 ,则代数式
,则代数式 的值为( )
的值为( )
A. | B. | C. | D. |
如图,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC交AC于点D,若AC=2,则AD的长是( )
A. | B. |
C. -1 -1 | D. +1 +1 |





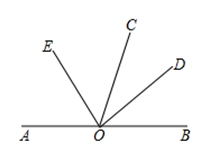
 是直线
是直线 上一点,
上一点,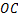 为任一条射线,
为任一条射线,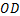 平分
平分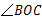 ,
,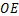 平分
平分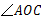 .
.
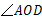 与
与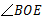 的补角;
的补角; 与
与 具有怎样的数量关系.
具有怎样的数量关系.