题目内容
【题目】如图1,某社会实践活动小组实地测量两岸互相平行的一段河的宽度,在河的南岸边点A处,测得河的北岸边点B在其北偏东45°方向,然后向西走60m到达C点,测得点B在点C的北偏东60°方向,如图2.
(1)求∠CBA的度数.
(2)求出这段河的宽(结果精确到1m,备用数据 ![]() ≈1.41,
≈1.41, ![]() ≈1.73).
≈1.73).
【答案】
(1)解:由题意得,∠BAD=45°,∠BCA=30°,
∴∠CBA=∠BAD﹣∠BCA=15°
(2)解:作BD⊥CA交CA的延长线于D,
设BD=xm,
∵∠BCA=30°,
∴CD= ![]() =
= ![]() x,
x,
∵∠BAD=45°,
∴AD=BD=x,
则 ![]() x﹣x=60,
x﹣x=60,
解得x= ![]() ≈82,
≈82,
答:这段河的宽约为82m.
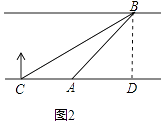
【解析】本题考查的是解直角三角形的应用﹣方向角问题,正确标注方向角、熟记锐角三角函数的定义是解题的关键.(1)根据三角形的外角的性质、结合题意计算即可;(2)作BD⊥CA交CA的延长线于D,设BD=xm,根据正切的定义用x表示出CD、AD,根据题意列出方程,解方程即可.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目