题目内容
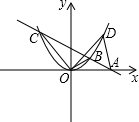 如图,直线AB过x轴上的点A(2,0),且与抛物线y=ax2相交于B、C两点,B点坐标为(1,1).
如图,直线AB过x轴上的点A(2,0),且与抛物线y=ax2相交于B、C两点,B点坐标为(1,1).(1)求直线和抛物线所表示的函数表达式;
(2)在抛物线上是否存在一点D,使得S△OAD=S△OBC?若不存在,说明理由;若存在,请求出点D的坐标,与同伴交流.
分析:(1)已知直线AB经过A(2,0),B(1,1),设直线表达式为y=ax+b,可求直线解析式;将B(1,1)代入抛物线y=ax2可求抛物线解析式;
(2)已知A,B,C三点坐标,根据作差法可求△OBC的面积,在△DOA中,已知面积和底OA,可求OA上的高,即D点纵坐标,代入抛物线解析式求横坐标,得出D点坐标.
(2)已知A,B,C三点坐标,根据作差法可求△OBC的面积,在△DOA中,已知面积和底OA,可求OA上的高,即D点纵坐标,代入抛物线解析式求横坐标,得出D点坐标.
解答:解:(1)设直线表达式为y=ax+b.
∵A(2,0),B(1,1)都在y=ax+b的图象上,
∴
.
∴直线AB的表达式y=-x+2.
∵点B(1,1)在y=ax2的图象上,
∴a=1,其表达式为y=x2.
(2)∵
,
解得
或
,
∴点C坐标为(-2,4),设D(a,a2).
∴S△OAD=
|OA|•|yD|=
×2•a2=a2.
∴S△BOC=S△AOC-S△OAB=
×2×4-
×2×1=3.
∵S△BOC=S△OAD,
∴a2=3,
即a=±
.
∴D点坐标为(
,3),(-
,3).
∵A(2,0),B(1,1)都在y=ax+b的图象上,
∴
|
∴直线AB的表达式y=-x+2.
∵点B(1,1)在y=ax2的图象上,
∴a=1,其表达式为y=x2.
(2)∵
|
解得
|
|
∴点C坐标为(-2,4),设D(a,a2).
∴S△OAD=
| 1 |
| 2 |
| 1 |
| 2 |
∴S△BOC=S△AOC-S△OAB=
| 1 |
| 2 |
| 1 |
| 2 |
∵S△BOC=S△OAD,
∴a2=3,
即a=±
| 3 |
∴D点坐标为(
| 3 |
| 3 |
点评:本题考查了一次函数、二次函数解析式的求法,要求会用点的坐标表示三角形的面积,从而求出符合条件的点坐标.

练习册系列答案
相关题目
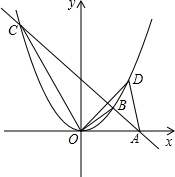 标是(1,1),
标是(1,1), 如图,直线AB过x轴上的点B(4,0),且与抛物线y=ax2交于A、C两点,已知A(2,2).
如图,直线AB过x轴上的点B(4,0),且与抛物线y=ax2交于A、C两点,已知A(2,2).
