题目内容
【题目】如图,在四边形![]() 中,
中,![]() 是对角线,
是对角线,![]() ,
,![]() ,延长
,延长![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.

(1)求证:![]() ;
;
(2)若![]() ,求
,求![]() 的值;
的值;
(3)过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() .设
.设![]() ,点
,点![]() 是直线
是直线![]() 上的动点,当
上的动点,当![]() 的值最小时,点
的值最小时,点![]() 与点
与点![]() 是否可能重合?若可能,请说明理由并求此时
是否可能重合?若可能,请说明理由并求此时![]() 的值(用含
的值(用含![]() 的式子表示);若不可能,请说明理由.
的式子表示);若不可能,请说明理由.
【答案】(1)见解析;(2)![]() ;(3)可以重合,理由见解析,
;(3)可以重合,理由见解析,![]() 的最小值为
的最小值为![]() .
.
【解析】
(1)运用HL证明![]() 即可得到结论;
即可得到结论;
(2)根据已知条件可证出AB=BE,从而可得∠BAE=45°,再由角平分线的定义可得∠BAC的度数;
(3)连接![]() ,连接
,连接![]() ,延长
,延长![]() 交
交![]() 的延长线于点
的延长线于点![]() .证明点
.证明点![]() 与点
与点![]() 关于直线
关于直线![]() 成轴对称,也即点
成轴对称,也即点![]() 、点
、点![]() 、点
、点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() ,这三点共线,也即
,这三点共线,也即![]() 的值最小时,点
的值最小时,点![]() 与点
与点![]() 重合.再证明
重合.再证明![]() 为等边三角形即可得到结论.
为等边三角形即可得到结论.
(1)证明:![]() ,
,
![]() ,
,![]() ,
,
![]() .
.
![]() .
.
(2)![]() ,
,
又![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
![]() .
.
![]() ,
,
![]() .
.
由(1)得![]() ,
,
![]() .
.
![]() .
.
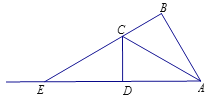
(3)当![]() 的值最小时,点
的值最小时,点![]() 与点
与点![]() 可以重合,理由如下:
可以重合,理由如下:
![]() ,
,
![]() ,
,![]() .
.
![]() ,
,
![]() .
.
![]() .
.
![]() .
.
由(1)得,![]() ,
,
![]() ,
,
![]() .即
.即![]() 平分
平分![]() .
.
又![]() ,
,![]() ,
,
![]() .
.
连接![]() ,连接
,连接![]() ,延长
,延长![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.
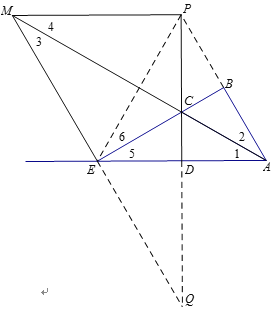
设![]() ,则
,则![]() .
.
在![]() 中,
中,![]() .
.
在![]() 中,
中,![]() .
.
![]() ,
,
![]()
![]() .
.
![]() ,
,
![]() .
.
当![]() 时,
时,
![]() ,
,![]() ,
,
![]() .
.
![]() .
.
即点![]() 与点
与点![]() 关于直线
关于直线![]() 成轴对称,也即点
成轴对称,也即点![]() 、点
、点![]() 、点
、点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() ,这三点共线,也即
,这三点共线,也即![]() 的值最小时,点
的值最小时,点![]() 与点
与点![]() 重合.
重合.
因为当![]() 时,
时,![]() ,也即
,也即![]() .
.
所以,当![]() 时,
时,![]() 取最小值时的点
取最小值时的点![]() 与点
与点![]() 重合.
重合.
此时![]() 的最小值即为
的最小值即为![]() .
.
![]() ,
,![]() ,
,![]() ,
,
![]() .
.
![]() .
.
![]() .
.
![]() ,
,![]() ,
,![]() 三点共线.
三点共线.
当![]() 时,在
时,在![]() 中,
中,
![]() .
.
∴ ∠EPA=60°.
![]() 为等边三角形
为等边三角形
.![]() ,
,
![]() .
.
![]() .
.
![]() ,
,
![]() .
.
![]() 的最小值为
的最小值为![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目