题目内容
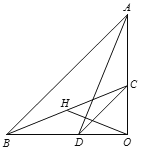
【题目】如图,△AOB和△COD均为等腰直角三角形,∠AOB=∠COD=90°,点C、D分别在边OA、OB上的点.连接AD,BC,点H为BC中点,连接OH.


(1)如图1,求证:OH=![]() AD,OH⊥AD;
AD,OH⊥AD;
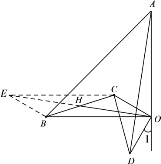
(2)将△COD绕点O旋转到图2所示位置时,⑴中结论是否仍成立?若成立,证明你的结论;若不成立,请说明理由.
【答案】(1)见解析;(2)成立,证明见解析
【解析】
(1)只要证明△AOD≌△BOC(SAS),即可解决问题;
(2)如图2中,结论:OH=![]() AD,OH⊥AD.延长OH到E,使得HE=OH,连接BE,证明△BEH≌△CHO(SAS),可得OE=2OH,∠EBC=∠BCO,证明△BEO≌△ODA(SAS)即可解决问题;
AD,OH⊥AD.延长OH到E,使得HE=OH,连接BE,证明△BEH≌△CHO(SAS),可得OE=2OH,∠EBC=∠BCO,证明△BEO≌△ODA(SAS)即可解决问题;
(1)∵△OAB与△OCD为等腰直角三角形,∠AOB=∠COD=90°.
∴OC=OD,OA=OB
在△AOD与△BOC中
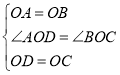
∴△AOD≌△BOC(SAS)
∴∠ADO=∠BCO,∠OAD=∠OBC,BC=AD
∵点H是BC的中点,∠AOB=90°
∴OH=HB=![]()
∴∠OBH=∠HOB=∠OAD,OH=![]()
∵∠OAD+∠ADO=90°
∴∠ADO+∠BOH=90°
∴OH⊥AD
(2)(1)中结论成立;如图,延长OH到E,使得HE=OH,连接BE,CE
∵CH=BH
∴四边形BOCE是平行四边形
∴BE=OC,EB∥OC,OH=![]() OE
OE
∴∠EBO+∠COB=180°
∵∠COB+∠BOD=90°,∠BOD+∠1=90°
∴∠1=∠COB
∵∠AOD+∠1=180°
∴∠AOD=∠EBO
∴△BEO≌△ODA
∴∠EOB=∠DAO,OE=AD
∴OH=![]() AD
AD
∴∠DAO+∠AOH=∠EOB+∠AOH=90°
∴OH⊥AD
【点晴】
本题属于几何变换综合题,考查了旋转变换,等腰直角三角形的性质,全等三角形的判定和性质,三角形三边关系等知识,构造全等三角形解决问题是解题的关键.

【题目】某公司在销售一种产品进价为10元的产品时,每年总支出为10万元(不含进货支出).经过若干年销售得知,年销售量![]() (万件)是销售单价
(万件)是销售单价![]() (元)的一次函数,并得到如下部分数据:
(元)的一次函数,并得到如下部分数据:
销售单价 | 12 | 14 | 16 | 18 |
年销售量 | 7 | 6 | 5 | 4 |
(1)求出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)写出该公司销售这种产品的年利润![]() (万元)关于销售单价
(万元)关于销售单价![]() (元)的函数关系式;当销售单价
(元)的函数关系式;当销售单价![]() 为何值时,年利润最大?
为何值时,年利润最大?
(3)试通过(2)中的函数关系式及其大致图象,帮助该公司确定产品的销售单价范围,使年利润不低于20万元(请直接写出销售单价![]() 的范围).
的范围).