题目内容
如图,∠BAC=110°,若MP和NQ分别垂直平分AB和AC,则∠PAQ的度数是
- A.20°
- B.40°
- C.50°
- D.60°
B
分析:由∠BAC的大小可得∠B与∠C的和,再由垂直平分线,可得∠BAP=∠B,∠QAC=∠C,进而可得∠PAQ的大小.
解答:∵∠BAC=110°,
∴∠B+∠C=70°,
又MP,NQ为AB,AC的垂直平分线,
∴∠BAP=∠B,∠QAC=∠C,
∴∠BAP+∠CAQ=70°,
∴∠PAQ=∠BAC-∠BAP-∠CAQ=110°-70°=40°
故选B.
点评:本题考查了线段垂直平分线的性质;要熟练掌握垂直平分线的性质,能够求解一些简单的计算问题.
分析:由∠BAC的大小可得∠B与∠C的和,再由垂直平分线,可得∠BAP=∠B,∠QAC=∠C,进而可得∠PAQ的大小.
解答:∵∠BAC=110°,
∴∠B+∠C=70°,
又MP,NQ为AB,AC的垂直平分线,
∴∠BAP=∠B,∠QAC=∠C,
∴∠BAP+∠CAQ=70°,
∴∠PAQ=∠BAC-∠BAP-∠CAQ=110°-70°=40°
故选B.
点评:本题考查了线段垂直平分线的性质;要熟练掌握垂直平分线的性质,能够求解一些简单的计算问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

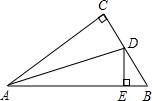 如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,且DE=4.8cm,BC=11.2cm,则BD=
如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,且DE=4.8cm,BC=11.2cm,则BD=
