题目内容
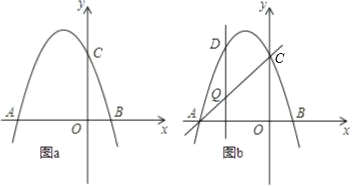
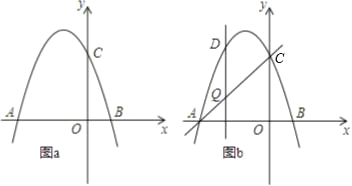
【题目】如图,抛物线y=﹣x2+bx+c交x轴于点A(﹣3,0)和点B,交y轴于点C(0,3).
(1)求抛物线的函数表达式;
(2)若点P在抛物线上,且S△AOP=4SBOC,求点P的坐标;
(3)如图b,设点Q是线段AC上的一动点,作DQ⊥x轴,交抛物线于点D,求线段DQ长度的最大值.
【答案】(1)y=﹣x2﹣2x+3(2)(﹣1,4)或(﹣1+2![]() ,﹣4)或(﹣1﹣2
,﹣4)或(﹣1﹣2![]() ,﹣4)(3)
,﹣4)(3)![]()
【解析】
试题分析:(1)把点A、C的坐标分别代入函数解析式,列出关于系数的方程组,通过解方程组求得系数的值;
(2)设P点坐标为(x,﹣x2﹣2x+3),根据S△AOP=4S△BOC列出关于x的方程,解方程求出x的值,进而得到点P的坐标;
(3)先运用待定系数法求出直线AC的解析式为y=x+3,再设Q点坐标为(x,x+3),则D点坐标为(x,x2+2x﹣3),然后用含x的代数式表示QD,根据二次函数的性质即可求出线段QD长度的最大值.
试题解析:(1)把A(﹣3,0),C(0,3)代入y=﹣x2+bx+c,得
![]() ,
,
解得![]() .
.
故该抛物线的解析式为:y=﹣x2﹣2x+3.
(2)由(1)知,该抛物线的解析式为y=﹣x2﹣2x+3,则易得B(1,0).
∵S△AOP=4S△BOC,
∴![]() ×3×|﹣x2﹣2x+3|=4×
×3×|﹣x2﹣2x+3|=4×![]() ×1×3.
×1×3.
整理,得(x+1)2=0或x2+2x﹣7=0,
解得x=﹣1或x=﹣1±2![]() .
.
则符合条件的点P的坐标为:(﹣1,4)或(﹣1+2![]() ,﹣4)或(﹣1﹣2
,﹣4)或(﹣1﹣2![]() ,﹣4);
,﹣4);
(3)设直线AC的解析式为y=kx+t,将A(﹣3,0),C(0,3)代入,
得![]() ,
,
解得![]() .
.
即直线AC的解析式为y=x+3.
设Q点坐标为(x,x+3),(﹣3≤x≤0),则D点坐标为(x,﹣x2﹣2x+3),
QD=(﹣x2﹣2x+3)﹣(x+3)=﹣x2﹣3x=﹣(x+![]() )2+
)2+![]() ,
,
∴当x=﹣![]() 时,QD有最大值
时,QD有最大值![]() .
.

 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案【题目】表记录了甲、乙、丙、丁四名跳远运动员选拔赛成绩的平均数x与方差s2,根据表中数据,要从中选择一名成绩好又发挥稳定的运动员参加比赛,应该选择( )
甲 | 乙 | 丙 | 丁 | |
平均数x/cm | 561 | 560 | 561 | 560 |
方差s2 | 3.5 | 3.5 | 15.5 | 16.5 |
A.甲B.乙C.丙D.丁