题目内容
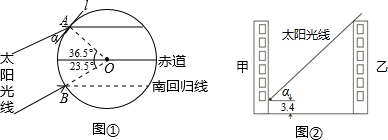
图①,②是晓东同学在进行“居民楼高度、楼间距对住户采光影响问题”的研究时画的两个示意图.请你阅读相关文字,解答下面的问题.(1)图①是太阳光线与地面所成角度的示意图.冬至日正午时刻,太阳光线直射在南回归线(南纬23.5°)B地上.在地处北纬36.5°的A地,太阳光线与地面水平线l所成的角为α,试借助图①,求α的度数;
(2)图②是乙楼高度、楼间距对甲楼采光影响的示意图.甲楼地处A地,其二层住户的南面窗户下沿距地面3.4米.现要在甲楼正南面建一幢高度为22.3米的乙楼,为不影响甲楼二层住户(一层为车库)的采光,两楼之间的距离至少应为多少米?
分析:(1)如图①,由于太阳光线是平行的,根据平行线的性质,就可以求出α;
(2)过点D作DE⊥CF,垂足为E,在Rt△CDE中利用三角函数就可以求出DE,也就求出了两楼之间的距离.
(2)过点D作DE⊥CF,垂足为E,在Rt△CDE中利用三角函数就可以求出DE,也就求出了两楼之间的距离.
解答:解:(1)如图①,
∵太阳光线是平行的,
∴∠α+90°+36.5°+23.5°=180°,
∴∠α=30°;
(2)如图②,过点D作DE⊥CF,垂足为E.

在Rt△CDE中,CE=22.3-3.4=18.9(米),∠CDE=30°,
∴cot30°=
,
∴DE=CEcot30°=18.9×
≈32.7(米).
答:两楼之间的距离至少为32.7米.
∵太阳光线是平行的,
∴∠α+90°+36.5°+23.5°=180°,
∴∠α=30°;
(2)如图②,过点D作DE⊥CF,垂足为E.

在Rt△CDE中,CE=22.3-3.4=18.9(米),∠CDE=30°,
∴cot30°=
| DE |
| CE |
∴DE=CEcot30°=18.9×
| 3 |
答:两楼之间的距离至少为32.7米.
点评:本题考查了直角三角形的有关知识,构造直角三角形是解决本题关键,属于中等难度题目.

练习册系列答案
相关题目



